11 Deep Learning

11.1 Multilayer Neural Networks

Neural networks with multiple layers are increasingly used to attack a variety of complex problems under the umberella of Deep Learning (Angermueller and Stegle 2016).

In this final section we will explore the basics of Deep Learning for image classification using a set of images taken from the animated TV series Rick and Morty. For those unfamiliar with Rick and Morty, the series revolves around the adventures of Rick Sanchez, an alcoholic, arguably sociopathic scientist, and his neurotic grandson, Morty Smith. Although many scientists aspire to be like Rick, they’re usually more like a Jerry.

Our motivating goal in this section is to develop a image classification algorithm capable of telling us whether a given image contains Rick or not: a binary classification task with two classes, Rick or not Rick. For training purposes we have downloaded \(1000\) random images of Rick and \(1000\) random images without Rick from the website Master of All Science. We have also downloaded \(200\) validation images each of the Rick versus not Rick classes. These images can be found in the appropriate subdirectories in the folder {/RickandMorty/data/}.

11.1.1 Constructing layers in kerasR

A user friendly package for Deep Learning is available via keras, an application programming interface (API) written in Python, which uses either theano or tensorflow as a back-end. An R interface for keras is available in the form of kerasR.

Before we can use kerasR we first need to load the kerasR library in R (we also need to install keras and either theano and tensorflow).

library(kerasR)

## successfully loaded keras

library(reticulate)
library(grid)
library(jpeg)
set.seed(12345)

Now we come to specifying the model itself. Keras has an simple and intuitive way of specifying layers of a neural network, and kerasR makes good use of this. We first initialie the model:

mod <- Sequential()

This tells keras that we’re using the Sequential API i.e., with the first layer connected to the second, the second to the thrid and so forth, which duistuinguishes it from more complex networks possible using the Model API. Once we’ve specified a sequential model, we have to specifiy the layers of the neural network.

A standard layer of neurons can be specified using the {Dense} command; the first layer of our network must also include the dimension of the input. So, for example, if our input data was a vector of dimension \(1 \times 40\), we could add an input layer via:

mod$add(Dense(100, input_shape = c(1,40)))

We also need to specfy the activation function to the next level. This can be done via {Activation()}, so our snippet of code using a Rectified Linear Unit (relu) activation would look something like:

mod$add(Dense(100, input_shape = c(1,40)))
mod$add(Activation("relu"))

We could add another layer of 120 neurons in (adding activation functions):

mod$add(Dense(100, input_shape = c(1,40)))
mod$add(Activation("relu"))
mod$add(Dense(120))
mod$add(Activation("relu"))

Finally, we should add the output neurons. If we had, for example, a binary classification algorithm, we could have two nodes, with a sigmoid activation function. Our final model would look like:

mod$add(Dense(100, input_shape = c(1,40)))
mod$add(Activation("relu"))
mod$add(Dense(120))
mod$add(Activation("relu"))
mod$add(Dense(2))
mod$add(Activation("sigmoid"))

That’s it. Simple!

11.1.2 Reading in images

We can load images and plot them in R using the {readJPEG} and {grid.raster} functions respectively.

im <- readJPEG("data/RickandMorty/data/train/Rick/Rick_001.jpg")
grid.raster(im, interpolate=FALSE)

Each image is stored as a jpeg file with \(90 \times 160\) pixel resolution and \(3\) colour channels (RGB). The input data is therefore a tensor/array of dimension \(90 \times 160 \times 3\). Keras expects inputs in the form of Numpy arrays, and we can construct the training dataset by loading all \(1000\) Rick and all \(1000\) not Rick images. We first get a list of all the Rick images in the directory {train/Rick}:

files <- list.files(path = "data/RickandMorty/data/train/Rick/", pattern = "jpg")

We next preallocate an empty array to store these training images for the Rick and not Rick images (an array of dimension \(2000 \times 90 \times 160 \times 3\)):

trainX  <- array(0, dim=c(2000,90,160,3))

We can load images using the {readJPEG} function:

for (i in 1:1000){
  trainX[i,1:90,1:160,1:3] <- readJPEG(paste("data/RickandMorty/data/train/Rick/", files[i], sep=""))
}

Similarly, we can load the not Rick images and store in the same array:

files <- list.files(path = "data/RickandMorty/data/train/Morty/",pattern = "jpg")
for (i in 1001:2000){
  trainX[i,1:90,1:160,1:3] <- readJPEG(paste("data/RickandMorty/data/train/Morty/", files[i-1000], sep=""))
}

Next we can construct a vector of length \(2000\) containing the classification for each of these \(2000\) images e.g., \(0\) if the image is a Rick and \(1\) if it is not Rick. This is simple enough using the function {rbind}, as we know the first \(1000\) images were Rick and the second \(1000\) images not Rick. Since we are dealing with a classification algorithm, we next convert the data to binary categorical output (that is, a Rick is now represented as \([1, 0]\) and a not Rick is a \([0, 1]\)), which we can do using the {to_categorical} conversion function:

trainY <- to_categorical(rbind(matrix(0, 1000, 1), matrix(1, 1000, 1)), 2)

Obviously the \(2\) in the code snippet above informs us that we have \(2\) classes; we could just as easily perform classificaiton with more than \(2\) classes, for example if we wanted to classify Ricky, Morty or neither Rick or Morty.

Next we will load in the validation sets:

files <- list.files(path = "data/RickandMorty/data/validation/Rick/",pattern = "jpg")

validateX  <- array(0, dim=c(400,90,160,3))

for (i in 1:200){
  validateX[i,1:90,1:160,1:3] <- readJPEG(paste("data/RickandMorty/data/validation/Rick/", files[i], sep=""))
}

files <- list.files(path = "data/RickandMorty/data/validation/Morty/",pattern = "jpg")
for (i in 201:400){
  validateX[i,1:90,1:160,1:3] <- readJPEG(paste("data/RickandMorty/data/validation/Morty/", files[i-200], sep=""))
}
validateY <- to_categorical(rbind(matrix(0, 200, 1),matrix(1, 200, 1)),2)

11.1.3 Rick and Morty classifier using Deep Learning

Let us return to our example of image classification. Our data is slightly different to the usual inputs we’ve been dealing with: that is, we’re not dealing with an input vector, but instead have an image. In this case each image is a \(90 \times 160 \time 3\) array, so for our first layer we have to flatten this down. This can be done using {Flatten()}:

mod$add(Flatten(input_shape = c(90, 160, 3)))

This should turn our \(90 \times \160 \times 3\) input into a \(1 \times 43200\) node input. We now add an intermediate layer containing \(100\) neurons, connected to the input layer with rectified linear units ({relu}):

mod$add(Activation("relu"))
mod$add(Dense(100))

Finally we connect this layer over the final output layer (two neurons) with sigmoid activation: activation

mod$add(Activation("relu"))
mod$add(Dense(2))
mod$add(Activation("sigmoid"))

The complete model should look something like:

mod <- Sequential()
mod$add(Flatten(input_shape = c(90, 160, 3)))
mod$add(Activation("relu"))
mod$add(Dense(100))
mod$add(Activation("relu"))
mod$add(Dense(2))
mod$add(Activation("sigmoid"))

We can visualise this model using the {plot_model} function (Figure 11.1).

plot_model(mod,'images/DNN1.png')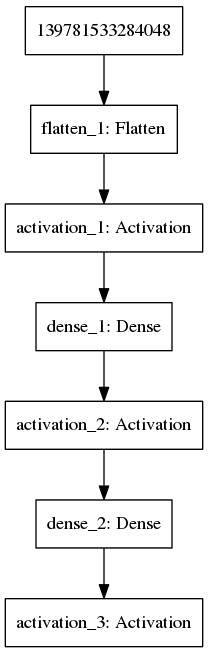

Figure 11.1: Example of a multilayer convolutional neural network

We can also print a summary of the network, for example to see how many parameters it has, using the {summary} function:

summary(mod)

## <keras.engine.sequential.Sequential>

In this case we see a total of \(4320302\) parameters. Next we need to compile and run the model. In this case we need to specify three things:

• A loss function, which specifies the objective function that the model will try to minimise. A number of existing loss functions are built into keras, including mean squared error (mean_squared_error) and categorical cross entropy (categorical_crossentropy). Since we are dealing with binary classification, we will use binary cross entropy (binary_crossentropy).

• An optimiser, which determines how the loss functin is optimised. Possible examples include stochastic gradient descent ({SGD()}) and Root Mean Square Propagation ({RMSprop()}).

• A list of metrics to return. These are additional summary statistics that keras evaluates and prints. For classification, a good choice would be accuracy.

We can compile this using {keras_compile}:

keras_compile(mod,  loss = 'binary_crossentropy', metrics = c('accuracy'), optimizer = RMSprop())

Finally the model can be fitted to the data. When doing so we additionally need to specify the validation set (if we have one), the batch size and the number of epochs, where an epoch is one forward pass and one backward pass of all the training examples and the batch size is the number of training examples in one forward/backward pass. You may want to go and get a tea whilst this is running!

keras_fit(mod, trainX, trainY, validation_data = list(validateX, validateY), batch_size = 32, epochs = 25, verbose = 1)

For this model we achieved an accuracy of \(0.5913\) on the validation dataset at epoch \(23\) (which had a corresponding accuracy of \(0.5938\) on the training set). Not great is an understatement. In fact it’s barely better than random (which would be \(0.5\), with \(1\) being perfect)! Let’s try adding in another layer to the network. In this case we add in a layer containing \(70\) neurons, connected with {relu} activations:

mod <- Sequential()
mod$add(Flatten(input_shape = c(90, 160, 3)))
mod$add(Activation("relu"))
mod$add(Dense(100))
mod$add(Activation("relu"))
mod$add(Dense(70))
mod$add(Activation("relu"))
mod$add(Dense(2))
mod$add(Activation("sigmoid"))
keras_compile(mod,  loss = 'binary_crossentropy', metrics = c('accuracy'), optimizer = RMSprop())
keras_fit(mod, trainX, trainY, validation_data = list(validateX, validateY), batch_size = 32, epochs = 25, verbose = 1)

We can again visualise the model:

plot_model(mod,'images/DNN2.png')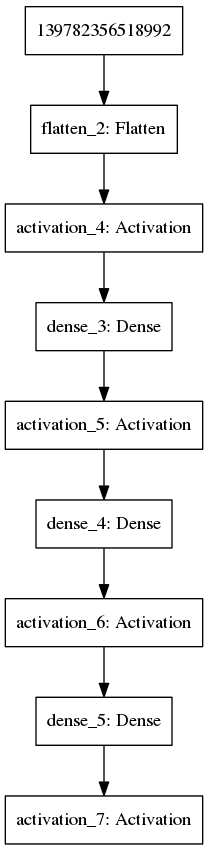

Figure 11.2: Example of a multilayer convolutional neural network

We get now get a validation accuracy of \(0.6238\) at epoch \(25\), with corresponding training accuracy of \(0.5767\). It’s an improvement, but it’s still pretty bad. We could try adding in extra layers, but it seems we’re getting nowhere fast, and will need to change tactic. We need to think a little about what the data actually is. In this case, we’re looking at a set of images. As Rick Sanchez can appear almost anywhere in the image, there’s no reason to think that a given input node should correspond in two different images, so it’s not surprising that the network did so badly. We need something that can extract out features from the image irregardless of where Rick is in the image. There are approaches build precicesly for image analysis that do just this: convolutional neural networks.

11.2 Convolutional neural networks

Convolutional neural networks essentially scan through an image and extract out a set of features. In multilayer neural networks, these features might then be passed on to deeper layers (other convolutional layers or standard neurons) as shown in Figure 11.3.

Figure 11.3: Example of a multilayer convolutional neural network

In kerasR we can add a convolutional layer using {Conv2D}. A multilayer convolutional neural network might look something like:

mod <- Sequential()
mod$add(Conv2D(filters = 20, kernel_size = c(5, 5),input_shape = c(90, 160, 3)))
mod$add(Activation("relu"))
mod$add(MaxPooling2D(pool_size=c(3, 3)))
mod$add(Conv2D(filters = 20, kernel_size = c(5, 5)))
mod$add(Activation("relu"))
mod$add(MaxPooling2D(pool_size=c(3, 3)))
mod$add(Conv2D(filters = 64, kernel_size = c(5, 5)))
mod$add(Activation("relu"))
mod$add(MaxPooling2D(pool_size=c(3, 3)))
mod$add(Flatten())
mod$add(Dense(100))
mod$add(Activation("relu"))
mod$add(Dropout(0.6))
mod$add(Dense(2))
mod$add(Activation("sigmoid"))

keras_compile(mod,  loss = 'binary_crossentropy', metrics = c('accuracy'), optimizer = RMSprop())
keras_fit(mod, trainX, trainY, validation_data = list(validateX, validateY), batch_size = 32, epochs = 25, verbose = 1)

Again we can visualise this network:

plot_model(mod,'images/DNN3.png')

Figure 11.4: Example of a multilayer convolutional neural network

Okay, so now we have achieved a better accuracy: we have an accuracy of \(0.8462\) on the validation dataset at epoch \(23\), with a training accuracy of \(0.9688\). Whilst this is still not great, it’s accurate enough to begin useuflly making predictions and visualising the results. We have a trained model for classification of Rick, we can use it to make predictions for images not present in either the training or validation datasets. First load in the new set of images, which can be found in the {predictions} subfolder:

files <- list.files(path = "data/RickandMorty/data/predictions/",pattern = "jpg")
predictX  <- array(0,dim=c(length(files),90,160,3))
for (i in 1:length(files)){
  x <- readJPEG(paste("data/RickandMorty/data/predictions/", files[i],sep=""))
  predictX[i,1:90,1:160,1:3] <- x[1:90,1:160,1:3]
}

A hard classification can be assigned using the {keras_predict_classes} function, whilst the probability of assignment to either class can be evaluated using {keras_predict_proba} (this can be useful for images that might be ambiguous).

probY <- keras_predict_proba(mod, predictX)
predictY <- keras_predict_classes(mod, predictX)

We can plot an example:

choice = 13
if (predictY[choice]==0) {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Rick',x = 0.4, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
} else {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Not Rick',x = 0.4, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
}

choice = 1
if (predictY[choice]==0) {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Rick',x = 0.4, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
} else {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Not Rick',x = 0.4, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
}

choice = 6
if (predictY[choice]==0) {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Rick',x = 0.4, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
} else {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Not Rick',x = 0.4, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
}

choice = 16
if (predictY[choice]==0) {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Rick',x = 0.4, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
} else {
  grid.raster(predictX[choice,1:90,1:160,1:3], interpolate=FALSE)
  grid.text(label='Not Rick: must be a Jerry',x = 0.2, y = 0.77,just = c("left", "top"), gp=gpar(fontsize=15, col="grey"))
}

11.2.1 Data augmentation

Although we saw some imporovements in the previous section using convolutional neural networks, the end results were not particularly convincing. After all, previous applications in the recognition of handwritten digits (0-9) showed above human accuracy, see e.g., Neural Networks and Deep Learning. Our accuracy of approximately \(80\) percent is nowhere near human levels of accuracy. So where are we gong wrong?

We should, of course, start by considering the number of parameters versus the size of the training dataset. In our final model we had \(69506\) parameters, and only \(2000\) training images, so it is perhaps not surprising that our model is doing relatively poorly. In previous examples of digit recognition more than \(10000\) images were used, whilst better known examples of Deep Learning for image classification make use of millions of images. Our task is also, arguably, a lot harder than digit recognition. After all, a handwritten \(0\) is relatively similar regardless of who wrote it. Rick Sanchez, on the other hand, can come in a diverse range of guises, with different postures, facial expressions, clothing, and even in pickle-Rick form. We may well need a vastly increased number of training; with more training data, we can begin to learn more robustly what features define a Rick. Whilst we could simply download more data from Master of All Science, an alternative approach is to atrificially increase our pool of training data by manipulating the images. For example, we could shear, warp or rotate some of the images in our training set; we could add noise and we could manipulate the colouring.

For example, when we artifically increase the training size in a Python implementation to \(10000\) we achieve an accuracy to \(0.8770\) on the validation data; when we artifically increase the training dataset to \(30000\) we pushed this above \(0.9\). Again, not quite human-level, but a reasonable accuracy, all things considered.

11.2.2 Asking more precise questions

Another way we could improve our accuracy is to ask more precise questions. In our application we have focused on what makes a Rick, and what makes a not Rick. Whilst there may be definable features for Rick, such as his hair and his white coat, the class not Rick is an amalgamation of all other characters and scenes in the series. A better approach would be to develop algorithms that classify Rick versus Morty. In this case we would need to tweak our training and validation datasets.

11.2.3 More complex networks

More complex learning algorithms can easily be built using keras using the Model class API rather than the Sequential API. This allows, for example, learning from multiple inputs and/or outputs, with more interconnection between different layers. We might, for example, want to include additional contextual information about the image that could serve to augment the predictions.

Another approach is to use transfer learning. This is where we make use of existing neural networks to make predictions on our specific datasets, usually fixing the top layers in place and fine tuning the lower layers to our dataset. For example, for image recognition we could make use of top perfoming neural networks on the ImageNet database. Whilst none of these networks would have been designed to identify Rick they would have been trained on millions of images, and the top levels would have been able to extract useful general features of an image.

11.3 Further reading

A particularly comprehensive introduction to Deep Learning can be found in the e-book Neural Networks and Deep Learning, written by Michael Nielsen.

Useful examples can also be found in the keras documentation.

Installing Python Linux Installing Python for Mac Python install via conda

Installing tensorflow Installing keras

Solutions to exercises can be found in appendix ??.

References

Angermueller, Tanel Pärnamaa, Christof, and Oliver Stegle. 2016. “Deep Learning for Computational Biology.” Molecular Systems Biology 12 (7): 878.