10 Supervised learning
Supervised learning refers to the general task of identifying how a set of annotated input data maps to a set of outcomes. In other words, it’s about learning functions from a labelled set of data, and using those functions for prediction. The labelled data typically consists of a matched pair of observations \(\{\mathbf{X},\mathbf{y}\}\), where \(\mathbf{X}\) (the input variables) usually denotes a matrix of (real-valued) explanatory variables, with \(\mathbf{X}_i\) denoting the \(i\)th column which contains observations for the \(i\)th variable, and \(\mathbf{y} = (y_1,\ldots,y_n)^\top\) (the output variable) denotes a vector of observations for a variable of interest[^The input variables need not be real values vectors, and could instead represent any measurement including graphs, text etc.]. Depending on the nature of the output variable, supervised learning is split into regression and classification tasks.
Within a regression setting, we aim to identify how the input variables map to the (continuous-valued) output variable(s). A simple example would involve measuring the population size of a bacterial culture, \(\mathbf{y} = (N_1,\ldots,N_n)^\top\), at a set of time points, \(\mathbf{X} = (t_1,\ldots,t_n)^\top\), and learning the function that maps from \(\mathbf{X}\) to \(\mathbf{y}\). Doing so should reveal something about the physical nature of the system, such as identifying the existence of distinct phases of growth. Correctly identifying these functions would also allow us to predict the output variable, \(\mathbf{y}^* = (N_i^*,\ldots,N_k^*)^\top\), at a new set of times, \(\mathbf{X}^* = (t_i,\ldots,t_k)^\top\).
Classification algorithms, on the other hand, deal with discrete-valued outputs. Here each observation in \(\mathbf{y} = (y_1,\ldots,y_n)\) can take on only a finite number of values. For example, we may have a measurment that indicates “infected” versus “uninfected”, which can be represented in binary, \(y_i \in [0,1]\). More generally we have data that falls into \(K\) classes e.g., “group 1” through to “group K”. As with regression, the aim is to identify how the (potentially continuous-valued) input variables map to the discrete set of class labels, and ultimately, assign labels to a new set of observations. Notable examples would be to identify how the expression levels of particular set of marker genes are predictive of a discrete phenotype.
In section 10.1 we briefly recap linear regression, and introduce nonlinear approaches to regression using Gaussian processes. We demonstrate the use of regression to predict gene expression values as a function of time, and how this can be used to inform us about the nature of the data, and as a way to make decisions about whether there are changed in gene expression over time.
In section 10.2 we introduce a variety of classification algorithms, starting with logistic regression (section 10), and demonstrate how such approaches can be used to predict pathogen infection status in Arabidopsis thaliana. By doing so we identify key marker genes indicative of pathogen growth. Finally, we note the limitations of linear classification algorithms, and introduce nonlinear approaches based on Gaussian processes (section 10.2.2).
10.1 Regression
In this section, we will make use of an existing dataset which captures the gene expression levels in the model plant Arabidopsis thaliana following innoculation with Botrytis cinerea (Windram et al. 2012), a necrotrophic pathogen considered to be one of the most important fungal plant pathogens due to its ability to cause disease in a range of plants. The dataset is a time series measuring the gene expression in Arabidopsis leaves following inoculation with Botrytis cinerea over a \(48\) hour time window at \(2\) hourly intervals.
The dataset is available from GEO (GSE39597) but a pre-processed version has been deposited in the {data} folder. The pre-processed data contains the expression levels of a set of \(163\) marker genes in tab delimited format. The fist row contains gene IDs for the marker genes. Column \(2\) contains the time points of observations, with column \(3\) containing a binary indication of infection status, evalutated according to the prescence of Botrytis cinerea Tubulin protein. All subsequent columns indicate (\(\log_2\)) normalised Arabidopsis gene expression values from microarrays (V4 TAIR V9 spotted cDNA array). The expression dataset itself contains two time series: the first \(24\) observations represent measurements of Arabidopsis gene expression in a control time series (uninfected), from \(2h\) through \(48h\) at \(2\)-hourly intervals, and therefore capture dynamic aspects natural plant processes, including circadian rhythms; the second set of \(24\) observations represents an infected dataset, again commencing \(2h\) after inoculation with Botyris cinerea through to \(48h\).
Within this section our output variable will typically be the expression level of a particular gene of interest, denoted \(\mathbf{y} =(y_1,\ldots,y_n)^\top\), with the explanatory variable being time, \(\mathbf{X} =(t_1,\ldots,t_n)^\top\). We can read the dataset into {R} as follows:
D <- read.csv(file = "data/Arabidopsis/Arabidopsis_Botrytis_transpose_3.csv", header = TRUE, sep = ",", row.names=1)We can also extract out the names of the variables (gene names), and the unique vector of measurment times:
genenames <- colnames(D)
Xs <- D$Time[1:24]Exercise 9.1. Plot the gene expression profiles to familiarise yourself with the data.
10.1.1 Linear regression
Recall that one of the simplest forms of regression, linear regression, assumes that the variable of interest, \(y\), depends on an explanatory variable, \(x\), via:
\(y = m x + c.\)
For a typical set of data, we have a vector of observations, \(\mathbf{y} = (y_1,y_2,\ldots,y_n)\) with a corresponding set of explanatory variables. For now we can assume that the explanatory variable is scalar, for example time (in hours), such that we have a set of observations, \(\mathbf{X} = (t_1,t_2,\ldots,t_n)\). Using linear regression we aim to infer the parameters \(m\) and \(c\), which will tell us something about the relationship between the two variables, and allow us to make predictions at a new set of locations, \(\mathbf{X}*\).
Within {R}, linear regression can be implemented via the {lm} function. In the example below, we perform linear regression for the gene expression of AT2G28890 as a function of time, using the infection time series only (hence we use only the first \(24\) datapoints):
lm(AT2G28890~Time, data = D[25:nrow(D),])##
## Call:
## lm(formula = AT2G28890 ~ Time, data = D[25:nrow(D), ])
##
## Coefficients:
## (Intercept) Time
## 10.14010 -0.04997Linear regression is also implemented within the {caret} package, allowing us to make use of its various other utilities. In fact, within {caret}, linear regression is performed by calling the function {lm}. In the example, below, we perform linear regression for AT2G28890, and predict the expression pattern for that gene using the {predict} function:
library(caret)## Loading required package: lattice## Loading required package: ggplot2library(mlbench)
set.seed(1)
geneindex <- which(genenames=="AT2G28890")
lrfit <- train(y~., data=data.frame(x=Xs,y=D[25:nrow(D),geneindex]), method = "lm")
predictedValues<-predict(lrfit)A summary of the model, including parameters, can be printed out to screen using the {summary} function:
summary(lrfit)##
## Call:
## lm(formula = .outcome ~ ., data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.77349 -0.17045 -0.01839 0.15795 0.63098
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.14010 0.13975 72.56 < 2e-16 ***
## x -0.04997 0.00489 -10.22 8.14e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3317 on 22 degrees of freedom
## Multiple R-squared: 0.826, Adjusted R-squared: 0.8181
## F-statistic: 104.4 on 1 and 22 DF, p-value: 8.136e-10Finally, we can fit a linear model to the control dataset, and plot the inferred results alongside the observation data:
lrfit2 <- train(y~., data=data.frame(x=Xs,y=D[1:24,geneindex]), method = "lm")
predictedValues2<-predict(lrfit2)
plot(Xs,D[25:nrow(D),geneindex],type="p",col="black",ylim=c(min(D[,geneindex])-0.2, max(D[,geneindex]+0.2)),main=genenames[geneindex])
points(Xs,D[1:24,geneindex],type="p",col="red")
points(Xs,predictedValues,type="l",col="black")
points(Xs,predictedValues2,type="l",col="red")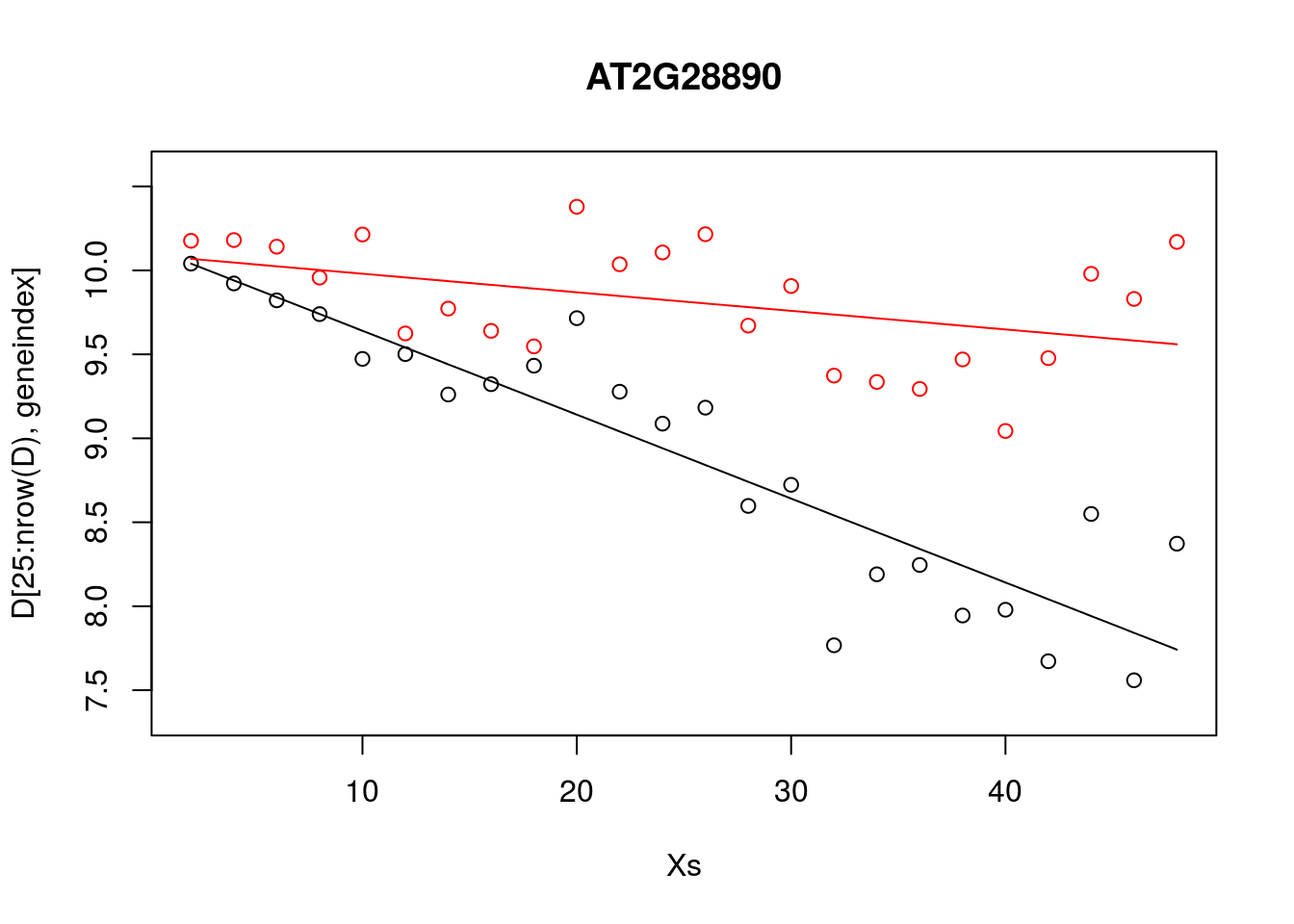
Whilst the model appeared to do resonably well at capturing the general trends in the datset, if we look at the control data (in red), you may notice that, visually, there appears to be more structure to the data than indicated by the model fit. Indeed, if we look AT2G28890 up on CircadianNET, we will see it is likely circadian in nature (\(p<5\times10^{-5}\)).
10.1.2 Polynomial regression
In general, linear models will not be appropriate for a large variety of datasets, particularly when the variables of interest are nonlinear. We can instead try to fit more complex models, such as a quadratic function, which has the following form:
\(y = m_1 x + m_2 x^2 + c,\)
where \(m = [m_1,m_2,c]\) represent the parameters we’re interested in inferring. An \(n\)th-order polynomial has the form:
\(y = \sum_{i=1}^{n} m_i x^i + c.\)
where \(m = [m_1,\ldots,m_n,c]\) are the free parameters. Within {R} we can infer more complex polynomials to the data using the {lm} package by calling the {poly} function when specififying the symbolic model. In the example below we fit a \(3\)rd order polynomial (the order of the polynomial is specified via the {degree} variable):
lrfit3 <- lm(y~poly(x,degree=3), data=data.frame(x=D[1:24,1],y=D[1:24,geneindex]))We can do this within {caret}: in the snippet, below, we fit \(3\)rd order polynomials to the control and infected datasets, and plot the fits alongside the data.
lrfit3 <- train(y~poly(x,degree=3), data=data.frame(x=D[1:24,1],y=D[1:24,geneindex]), method = "lm")
lrfit4 <- train(y~poly(x,degree=3), data=data.frame(x=D[25:nrow(D),1],y=D[25:nrow(D),geneindex]), method = "lm")
plot(Xs,D[25:nrow(D),geneindex],type="p",col="black",ylim=c(min(D[,geneindex])-0.2, max(D[,geneindex]+0.2)),main=genenames[geneindex])
points(Xs,D[1:24,geneindex],type="p",col="red")
lines(Xs,fitted(lrfit3),type="l",col="red")
lines(Xs,fitted(lrfit4),type="l",col="black")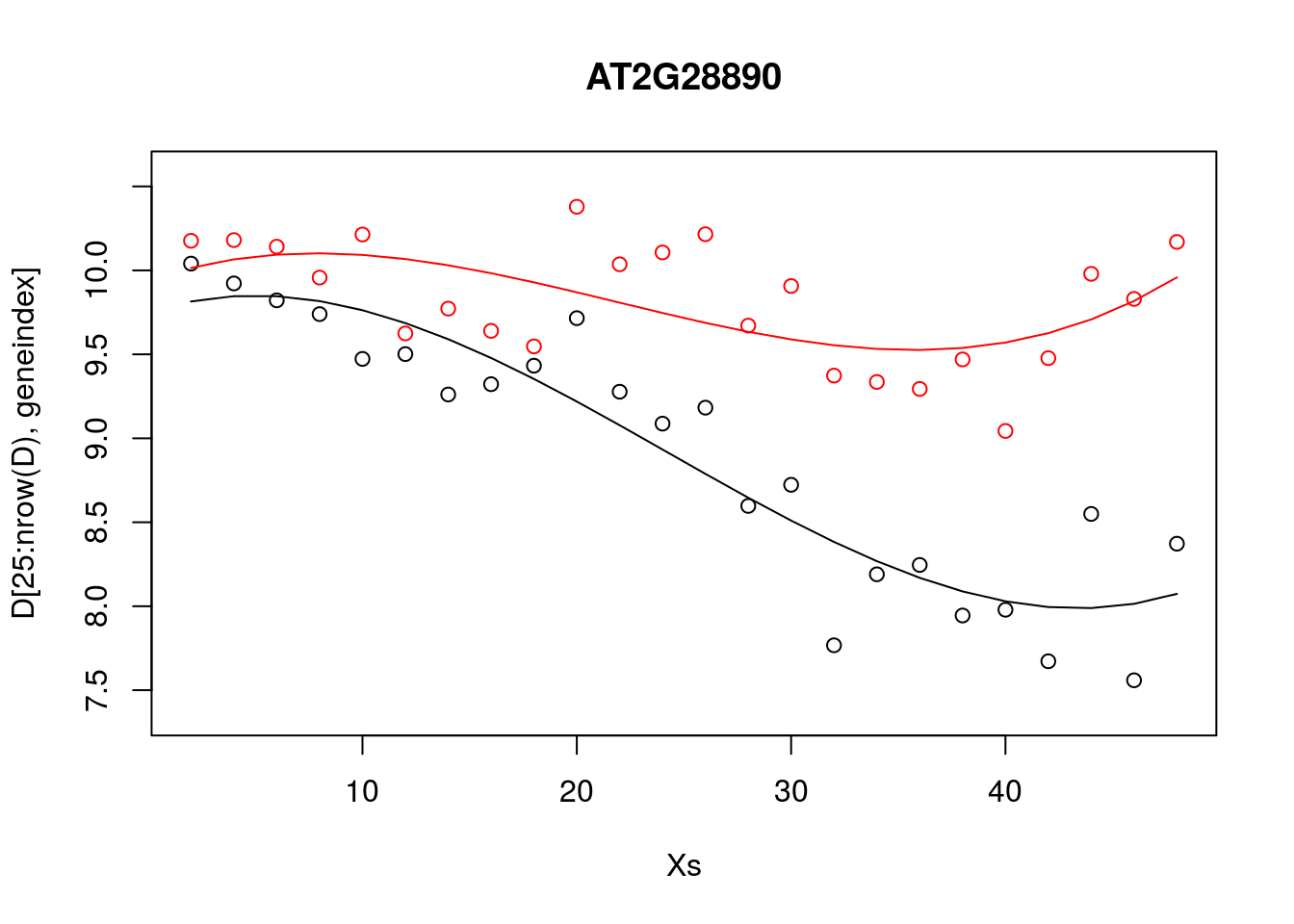
Note that, by eye, the fit appears to be a little better than for the linear regression model. Well, maybe! We can quantify the accuracy of the models by looking at the root-mean-square error (RMSE) on hold-out data (cross validation), defined as:
\(\mbox{RMSE} = \sqrt{\sum_{i=1}^n (\hat{y_i}-y_i)^2/n}\)
where \(\hat{y_i}\) is the predicted value and \(y_i\) the observed value of the \(i\)th (held out) datapoint. In previous sections we explicitly specified a set of training data and hold-out data (test data). If we do not specify this in {caret}, the data is split by default values.
Exercise 9.4. What happens if we fit a much higher order polynomial? Try fitting a polynomial with degree = 20 and plotting the result. As we increase the model complexity the fit appears to match much more closely to the observed data. However, intuitively we feel this is wrong. Whilst it may be possible that the data was generated by such complex polynomials, it’s far more likely that we are overfitting the data. We can evaluate how good the model really is by holding some data back and looking at the RMSE from bootstrapped samples. Try splitting the data into training and test datasets, and fitting polynomials of increasing complexity. Plot the RMSE on the training and the test datasets as a function of degree. How does the RMSE compare? Which model seems to be best?
10.1.3 Distributions of fits
In the previous section we explored fitting a polynomial function to the data. Recall that we can fit a \(4\)th order polynomial to the control datasets as follows:
lrfit3 <- lm(y~poly(x,degree=4), data=data.frame(x=D[1:24,1],y=D[1:24,geneindex]))
plot(Xs,D[1:24,geneindex],type="p",col="black",ylim=c(min(D[,geneindex])-0.2, max(D[,geneindex]+0.2)),main=genenames[geneindex])
lines(Xs,fitted(lrfit3),type="l",col="red")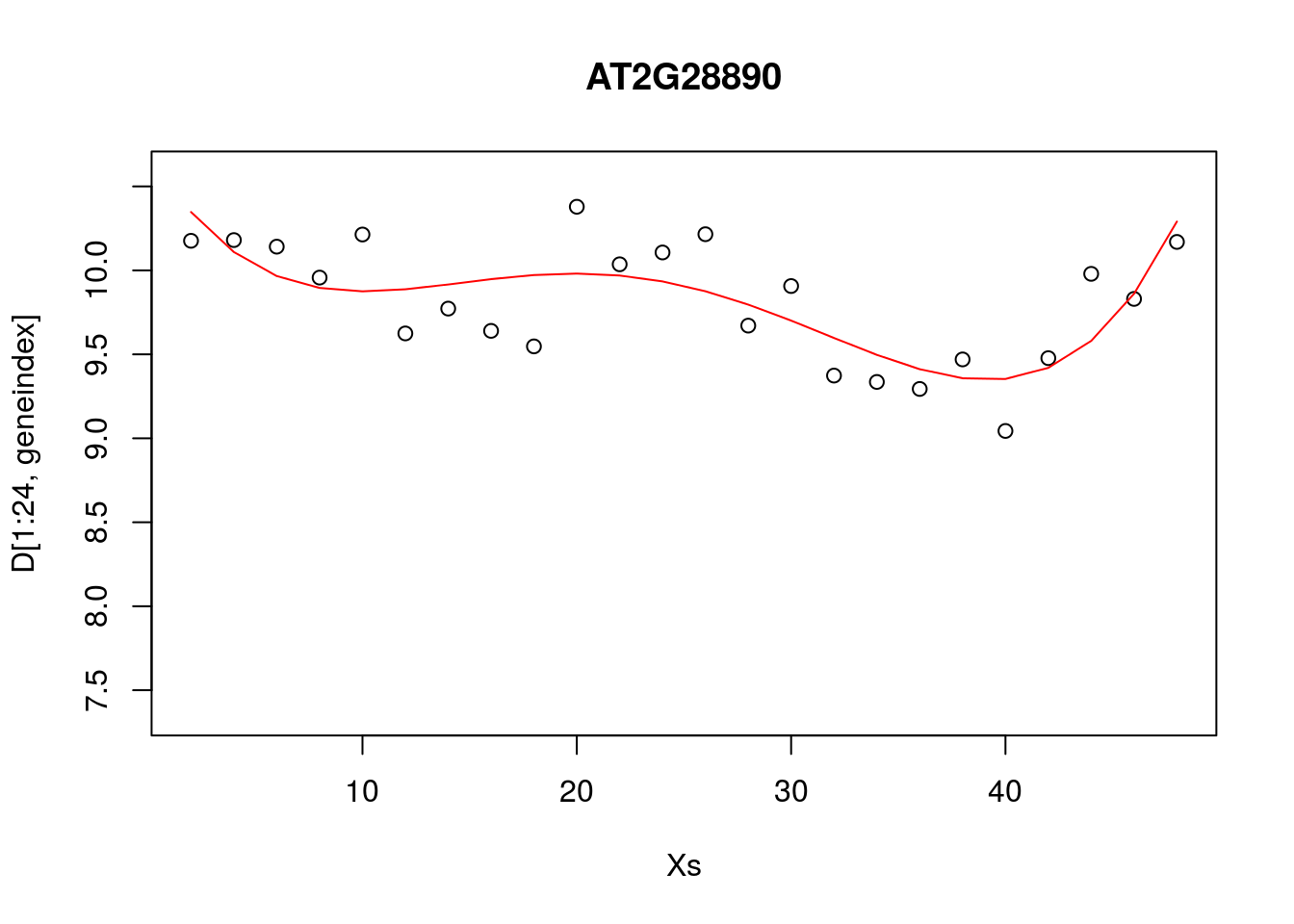
It looks reasonable, but how does it compare to the following shown in blue?
lrfit4 <- lrfit3
lrfit4$coefficients <- lrfit4$coefficients + 0.1*matrix(rnorm(length(lrfit4$coefficients)),length(lrfit4$coefficients));
pred1<-predict(lrfit4, data=data.frame(x=D[1:24,1],y=D[1:24,geneindex]))
plot(Xs,D[1:24,geneindex],type="p",col="black",ylim=c(min(D[,geneindex])-0.2, max(D[,geneindex]+0.2)),main=genenames[geneindex])
lines(Xs,fitted(lrfit3),type="l",col="red")
lines(Xs,pred1,type="l",col="blue")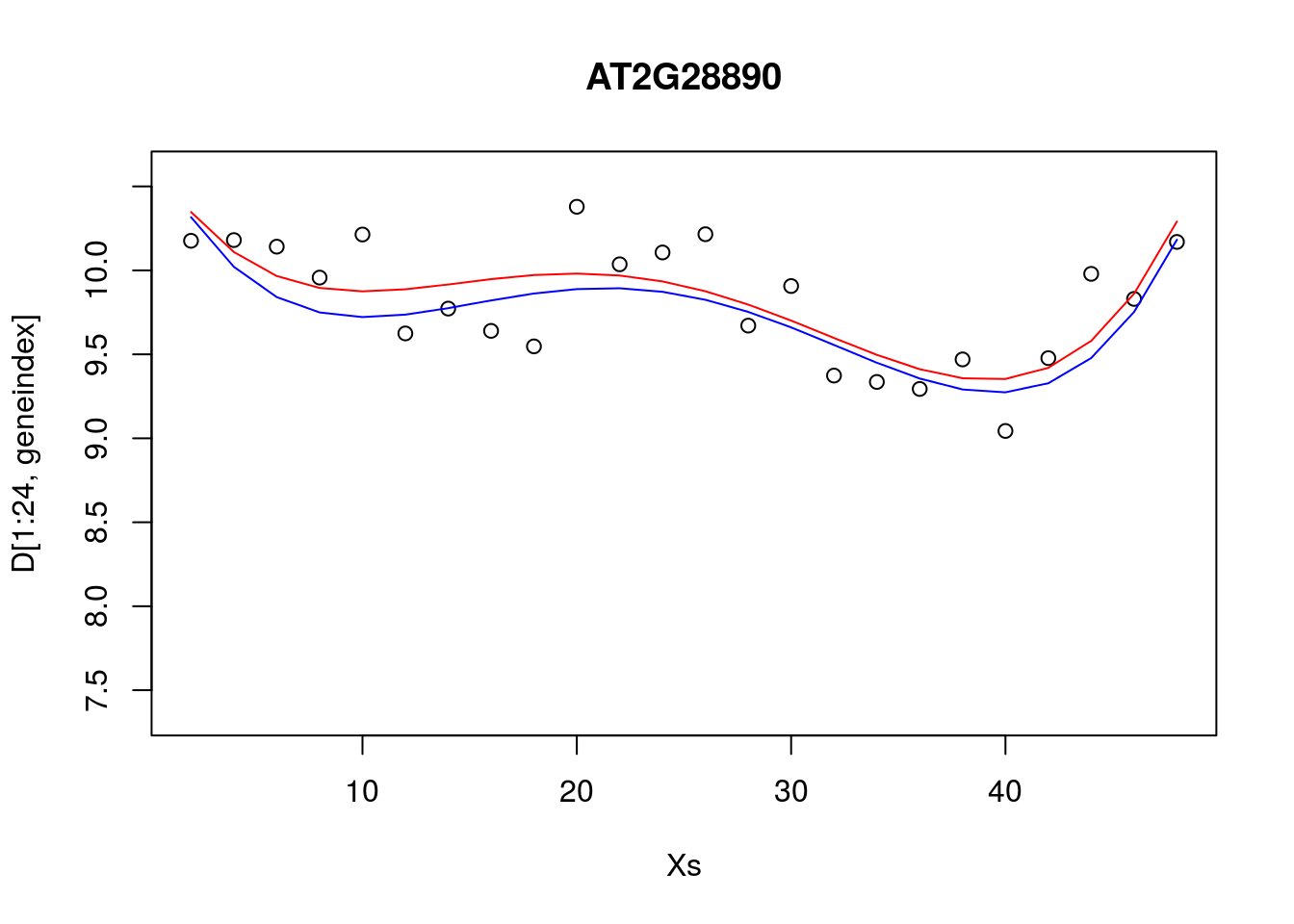
Our new fit was generated by slightly perturbing the optimised parameters via the addition of a small amount of noise. We can see that the new fit is almost as good, and will have a very similar SSE[^This should give us some intuition on the notion of over-fitting. For example, if we make a small perturbation to the parameters of a simpler model, the function will not change all that much; if the simpler model is doing a resonable job of explaining the data, then there may be no necessity of fitting a more complex one. On the other hand, if we made a small perturbation to the parameters of a more complex polynomial, the function may look drastically different. To explain the data with the more complex model would therefore require very specific sets of parameters]. In general, inferring a single fit to a model is prone to overfitting. A much better approach is to instead fit a distribution over fits. We can generate samples from a linear model using the {coef} function. To do so we must use the {lm} function directly, and not via the {caret} package.
library("arm")## Loading required package: MASS## Loading required package: Matrix## Loading required package: lme4##
## arm (Version 1.10-1, built: 2018-4-12)## Working directory is /home/participant/Course_Materials/intro-machine-learning-2019lrfit4 <- lm(y~poly(x,degree=4), data=data.frame(x=D[1:24,1],y=D[1:24,geneindex]))
simulate <- coef(sim(lrfit4))
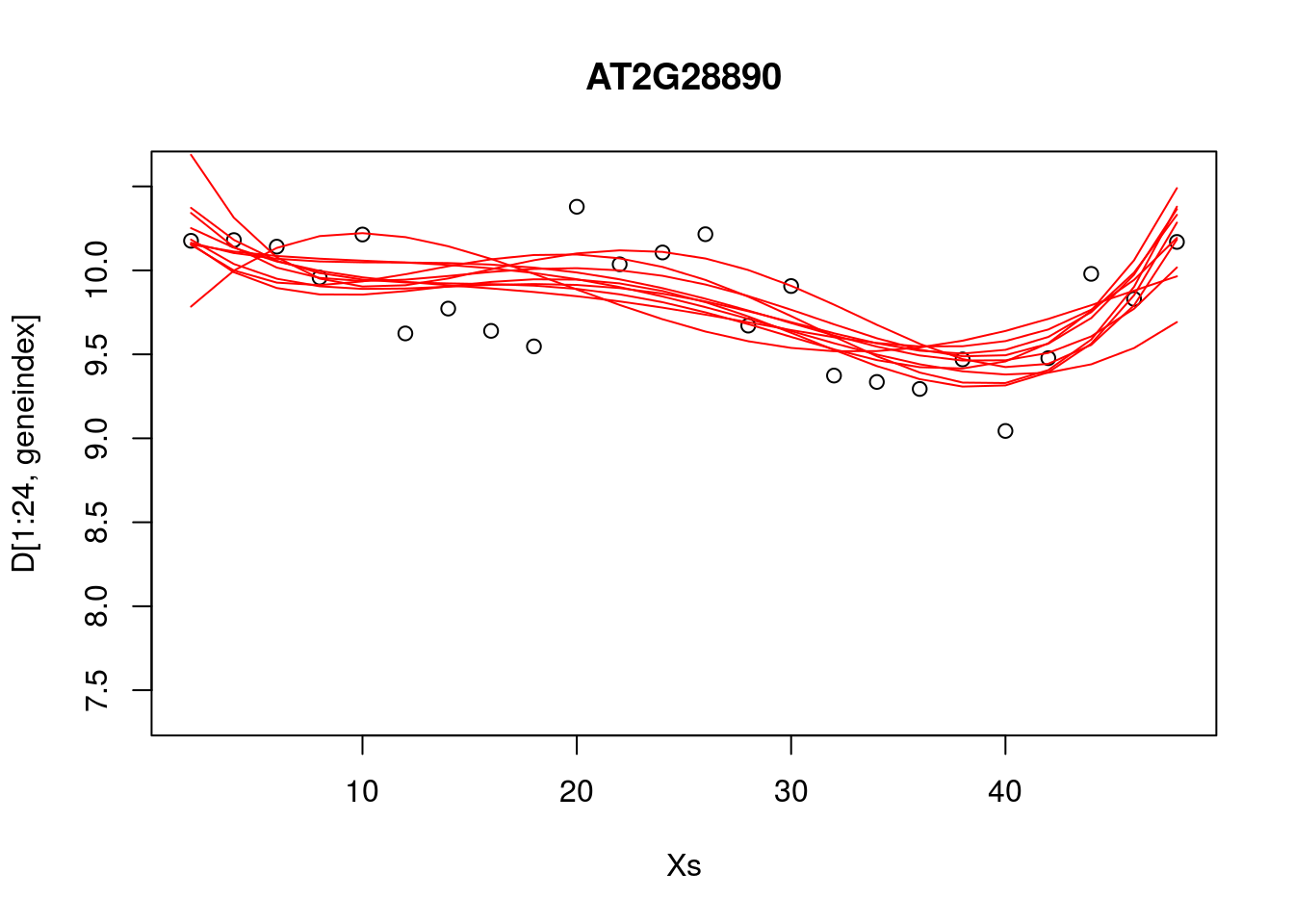
paramsamp <- head(simulate,10)This will sample model parameters that are likely to be explaining the dataset, in this case we have produced \(10\) different set of sample parameters. In the code, below, we plot these \(10\) sample polynomials:
plot(Xs,D[1:24,geneindex],type="p",col="black",ylim=c(min(D[,geneindex])-0.2, max(D[,geneindex]+0.2)),main=genenames[geneindex])
for (i in c(1,2,3,4,5,6,7,8,9,10)){
lrfit4$coefficients <- paramsamp[i,]
pred1<-predict(lrfit4, data=data.frame(x=D[1:24,1],y=D[1:24,geneindex]))
lines(Xs,pred1,type="l",col="red")
}
Alternatively, we can visualise the confidence bounds directly:
lrfit4 <- lm(y~poly(x,degree=4), data=data.frame(x=D[1:24,1],y=D[1:24,geneindex]))
pred1<-predict(lrfit4, interval="predict")## Warning in predict.lm(lrfit4, interval = "predict"): predictions on current data refer to _future_ responsesplot(Xs,D[1:24,geneindex],type="p",col="black",ylim=c(min(D[,geneindex])-0.2, max(D[,geneindex]+0.2)),main=genenames[geneindex])
lines(Xs,pred1[,1],type="l",col="red")
lines(Xs,pred1[,2],type="l",col="red")
lines(Xs,pred1[,3],type="l",col="red")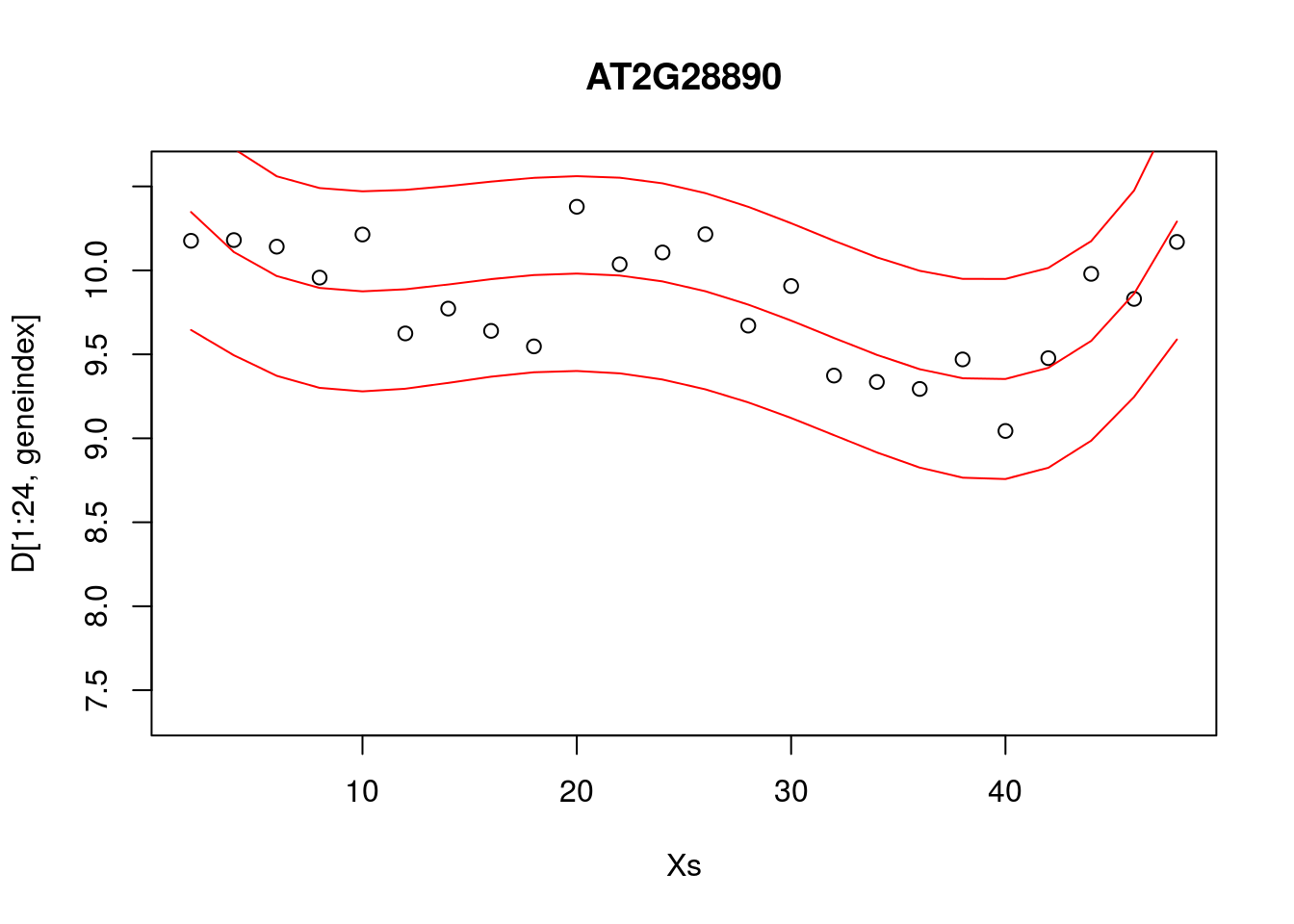
10.1.4 Gaussian process regression
In the previous section we briefly explored fitting multiple polynomials to our data. However, we still had to decide on the order of the polynomial beforehand. A far more powerful approach is Gaussian processes (GP) regression (Williams and Rasmussen 2006). Gaussian process regression represent a Bayesian nonparametric approach to regression capable of inferring nonlinear functions from a set of observations. Within a GP regression setting we assume the following model for the data:
\(y = f(\mathbf{X})\)
where \(f(\cdot)\) represents an unknown nonlinear function.
Formally, Gaussian processes are defined as a collections of random variables, any finite subset of which are jointly Gaussian distributed (Williams and Rasmussen 2006). The significance of this might not be immediately clear, and another way to think of GPs is as an infinite dimensional extension to the standard multivariate normal distribution. In the same way a Gaussian distribution is defined by its mean, \(\mathbf{\mu}\), and covaraiance matrix, \(\mathbf{K}\), a Gaussian processes is completely defined by its mean function, \(m(X)\), and covariance function, \(k(X,X^\prime)\), and we use the notation \(f(x) \sim \mathcal{GP}(m(x), k(x,x^\prime))\) to denote that \(f(X)\) is drawn from a Gaussian process prior.
As it is an infinite dimensional object, dealing directly with the GP prior is not feasible. However, we can make good use of the properties of a Gaussian distributions to sidestep this. Notably, the integral of a Gaussian distribution is itself a Gaussian distribution, which means that if we had a two-dimensional Gaussian distribution (defined over an x-axis and y-axis), we could integrate out the effect of y-axis to give us a (Gaussian) distribution over the x-axis. Gaussian processes share this property, which means that if we are interested only in the distribution of the function at a set of locations, \(\mathbf{X}\) and \(\mathbf{X}^*\), we can specify the distribution of the function over the entirity of the input domain (all of x), and analytically integrate out the effect at all other locations. This induces a natural prior distribution over the output variable that is, itself, Gaussian:
\[ \begin{eqnarray*} \begin{pmatrix}\mathbf{y}^\top\\ \mathbf{y^*}^\top \end{pmatrix} & \sim & N\left(\left[\begin{array}{c} \mathbf{0}\\ \mathbf{0}\\ \end{array}\right],\left[\begin{array}{ccc} K(\mathbf{x},\mathbf{x}) & K(\mathbf{x},\mathbf{x}^*)\\ K(\mathbf{x}^*,\mathbf{x}) & K(\mathbf{x}^*,\mathbf{x}^*) \\ \end{array}\right)\right] \end{eqnarray*} \]
Quite often we deal with noisy data where:
\(y = f(\mathbf{x}) + \varepsilon\),
and \(\varepsilon\) represents independent Gaussian noise. In this setting we are interested in inferring the function \(\mathbf{f}^*\) at \(\mathbf{X}*\) i.e., using the noise corrupted data to infer the underlying function, \(f(\cdot)\). To do so we note that a priori we have the following joint distribution:
\[ \begin{eqnarray*} \begin{pmatrix}\mathbf{y}^\top\\ \mathbf{f^*}^\top \end{pmatrix} & \sim & N\left(\left[\begin{array}{c} \mathbf{0}\\ \mathbf{0}\\ \end{array}\right],\left[\begin{array}{ccc} K(\mathbf{x},\mathbf{x})+\sigma_n^2 \mathbb{I} & K(\mathbf{x},\mathbf{x}^*)\\ K(\mathbf{x}^*,\mathbf{x}) & K(\mathbf{x}^*,\mathbf{x}^*) \\ \end{array}\right)\right] \end{eqnarray*} \]
10.1.4.1 Sampling from the prior
In the examples below we start by sampling from a GP prior as a way of illustrating what it is that we’re actualy doing. We first require a number of packages:
require(MASS)
require(plyr)## Loading required package: plyrrequire(reshape2)## Loading required package: reshape2require(ggplot2)Recall that the GP is completely defined by its mean function and covariance function. We can assume a zero-mean function without loss of generality. Until this point, we have not said much about what the covariance function is. In general, the covariance function encodes all information about the type of functions we’re interested in: is it smooth? Periodic? Does it have more complex structure? Does it branching? A good starting point, and the most commonly used covariance function, is the squared exponential covariance function:
\(k(X,X^\prime) = \sigma^2 \exp\biggl{(}\frac{(X-X^\prime)^2}{2l^2}\biggr{)}\).
This encodes for smooth functions (functions that are infinitely differentiable), and has two hyperparameters: a length-scale hyperparameter \(l\), which defines how fast the functions change over the input space (in our example this would time), and a process variance hyperparameter, \(\sigma\), which encodes the amplitude of the function (in our examples this represents roughly the amplitude of gene expression levels). In the snippet of code, below, we implement a squared exponential covariance function
covSE <- function(X1,X2,l=1,sig=1) {
K <- matrix(rep(0, length(X1)*length(X2)), nrow=length(X1))
for (i in 1:nrow(K)) {
for (j in 1:ncol(K)) {
K[i,j] <- sig^2*exp(-0.5*(abs(X1[i]-X2[j]))^2 /l^2)
}
}
return(K)
}To get an idea of what this means, we can generate samples from the GP prior at a set of defined positions along \(X\). Recall that due to the nature of GPs this is Gaussian distributed:
x.star <- seq(-5,5,len=500) ####Define a set of points at which to evaluate the functions
sigma <- covSE(x.star,x.star) ###Evaluate the covariance function at those locations, to give the covariance matrix.
y1 <- mvrnorm(1, rep(0, length(x.star)), sigma)
y2 <- mvrnorm(1, rep(0, length(x.star)), sigma)
y3 <- mvrnorm(1, rep(0, length(x.star)), sigma)
plot(y1,type = 'l',ylim=c(min(y1,y2,y3),max(y1,y2,y3)))
lines(y2)
lines(y3)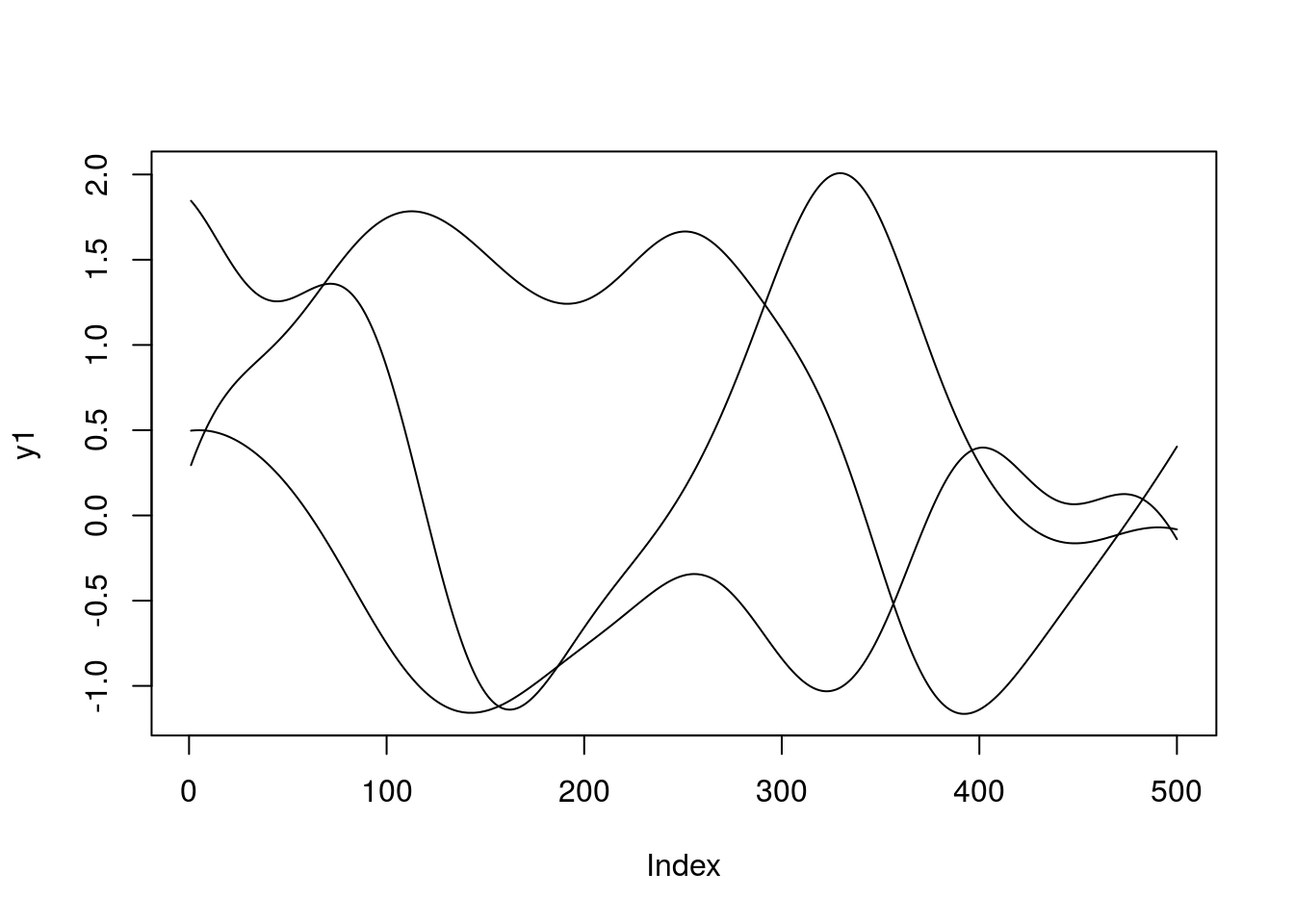
When we specify a GP, we are essentially encoding a distribution over a whole range of functions. Exactly how those functions behave depends upon the choice of covariance function and the hyperparameters. To get a feel for this, try changing the hyperparameters in the above code. What do the functions look like? A variety of other covariance functions exist, and can be found, with examples in the Kernel Cookbook.
Exercise 9.4 (optional): Try implementing another covariance function from the Kernel Cookbook and generating samples from the GP prior. Since we have already seen that some of our genes are circadian, a useuful covariance function to try would be the periodic covariance function.
10.1.4.2 Inference with GPs
We can generate samples from the GP prior, but what about inference? In linear regression we aimed to infer the parameters, \(m\) and \(a\). What is the GP doing during inference? Essentially, it’s representing the (unknown) function in terms of the observed data and the hyperparameters. Another way to look at it is that we have specified a prior distribution (encoding for all functions of a particular kind) over the input space; during inference in the noise-free case, we then discard all functions that don’t pass through those observations. During inference for noisy data we assign greater weight to those functions that pass close to our observed datapoints. Essentially we’re using the data to pin down a subset of the prior functions that behave in the appropriate way.
For the purpose of inference, we typically have a set of observations, \(\mathbf{X}\), and outputs \(\mathbf{y}\), and are interested in inferring the (unnoisy) values, \(\mathbf{f}^*\), at new set of test locations, \(\mathbf{X}^*\). We can infer a posterior distribution for \(\mathbf{f}^*\) using Bayes’ rule:
\(p(\mathbf{f}^* | \mathbf{X}, \mathbf{y}, \mathbf{X}^*) = \frac{p(\mathbf{y}, \mathbf{f}^* | \mathbf{X}, \mathbf{X}^*)}{p(\mathbf{y}|\mathbf{X})}.\)
A key advantage of GPs is that the preditive distribution is analytically tractible and has the following Gaussian form:
\(\mathbf{f}^* | \mathbf{X}, \mathbf{y}, \mathbf{X}* \sim \mathcal{N}(\hat{f}^*,\hat{K}^*)\)
where,
\(\hat{f}^* = K(\mathbf{X},\mathbf{X}^*)^\top(K(\mathbf{X},\mathbf{X})+\sigma^2\mathbb{I})^{-1} \mathbf{y}\),
\(\hat{K}^* = K(\mathbf{X}^*,\mathbf{X}^*)^{-1} - K(\mathbf{X},\mathbf{X}^*)^\top (K(\mathbf{X},\mathbf{X})+\sigma^2\mathbb{I})^{-1} K(\mathbf{X},\mathbf{X}^*)\).
To demonstrate this, let’s assume we have an unknown function we want to infer. In our example, for data generation, we will assume this to be \(y = \sin(X)\) as an illustrative example of a nonlinear function (although we know this, the GP will only ever see samples from this function, never the function itself). We might have some observations from this function at a set of input positions \(X\) e.g., one observation at \(x=-2\):
f <- data.frame(x=c(-2),
y=sin(c(-2)))We can infer a posterior GP (and plot this against the true underlying function in red):
x <- f$x
k.xx <- covSE(x,x)
k.xxs <- covSE(x,x.star)
k.xsx <- covSE(x.star,x)
k.xsxs <- covSE(x.star,x.star)
f.star.bar <- k.xsx%*%solve(k.xx)%*%f$y ###Mean
cov.f.star <- k.xsxs - k.xsx%*%solve(k.xx)%*%k.xxs ###Var
plot(x.star,sin(x.star),type = 'l',col="red",ylim=c(-2.2, 2.2))
points(f,type='o')
lines(x.star,f.star.bar,type = 'l')
lines(x.star,f.star.bar+2*sqrt(diag(cov.f.star)),type = 'l',pch=22, lty=2, col="black")
lines(x.star,f.star.bar-2*sqrt(diag(cov.f.star)),type = 'l',pch=22, lty=2, col="black")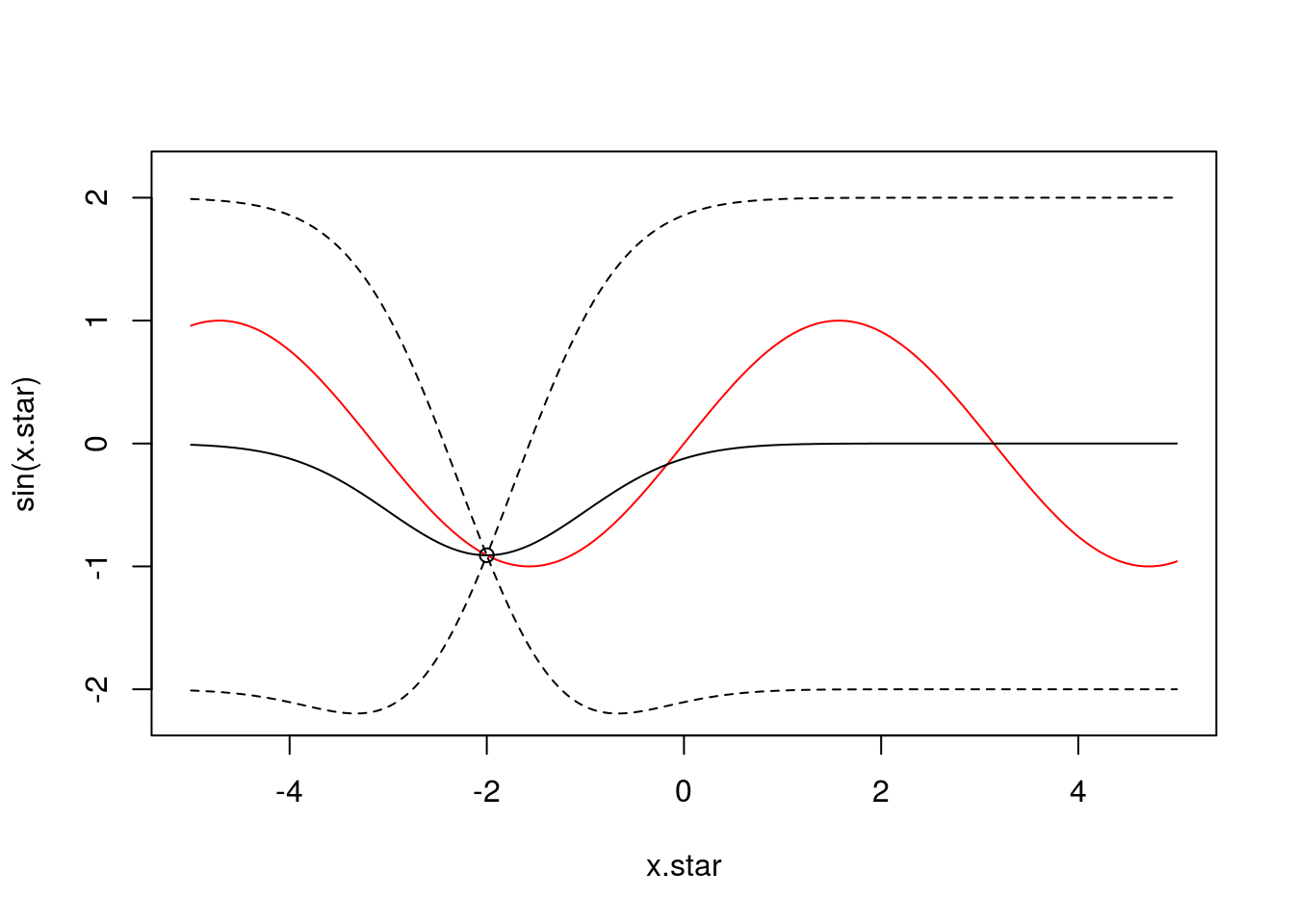
We can see that the GP has pinned down functions that pass close to the datapoint. Of course, at this stage, the fit is not particularly good, but that’s not surprising as we only had one observation. Crucially, we can see that the GP encodes the idea of uncertainty. Although the model fit is not particularly good, we can see exactly where it is no good.
Exercise 9.5 (optional): Try plotting some sample function from the posterior GP. Hint: these will be Gaussian distributed with mean {f.star.bar} and covariance {cov.f.star}.
Let’s start by adding more observations. Here’s what the posterior fit looks like if we include 4 observations (at \(x \in [-4,-2,0,1]\)):
f <- data.frame(x=c(-4,-2,0,1),
y=sin(c(-4,-2,0,1)))
x <- f$x
k.xx <- covSE(x,x)
k.xxs <- covSE(x,x.star)
k.xsx <- covSE(x.star,x)
k.xsxs <- covSE(x.star,x.star)
f.star.bar <- k.xsx%*%solve(k.xx)%*%f$y ###Mean
cov.f.star <- k.xsxs - k.xsx%*%solve(k.xx)%*%k.xxs ###Var
plot(x.star,sin(x.star),type = 'l',col="red",ylim=c(-2.2, 2.2))
points(f,type='o')
lines(x.star,f.star.bar,type = 'l')
lines(x.star,f.star.bar+2*sqrt(diag(cov.f.star)),type = 'l',pch=22, lty=2, col="black")
lines(x.star,f.star.bar-2*sqrt(diag(cov.f.star)),type = 'l',pch=22, lty=2, col="black")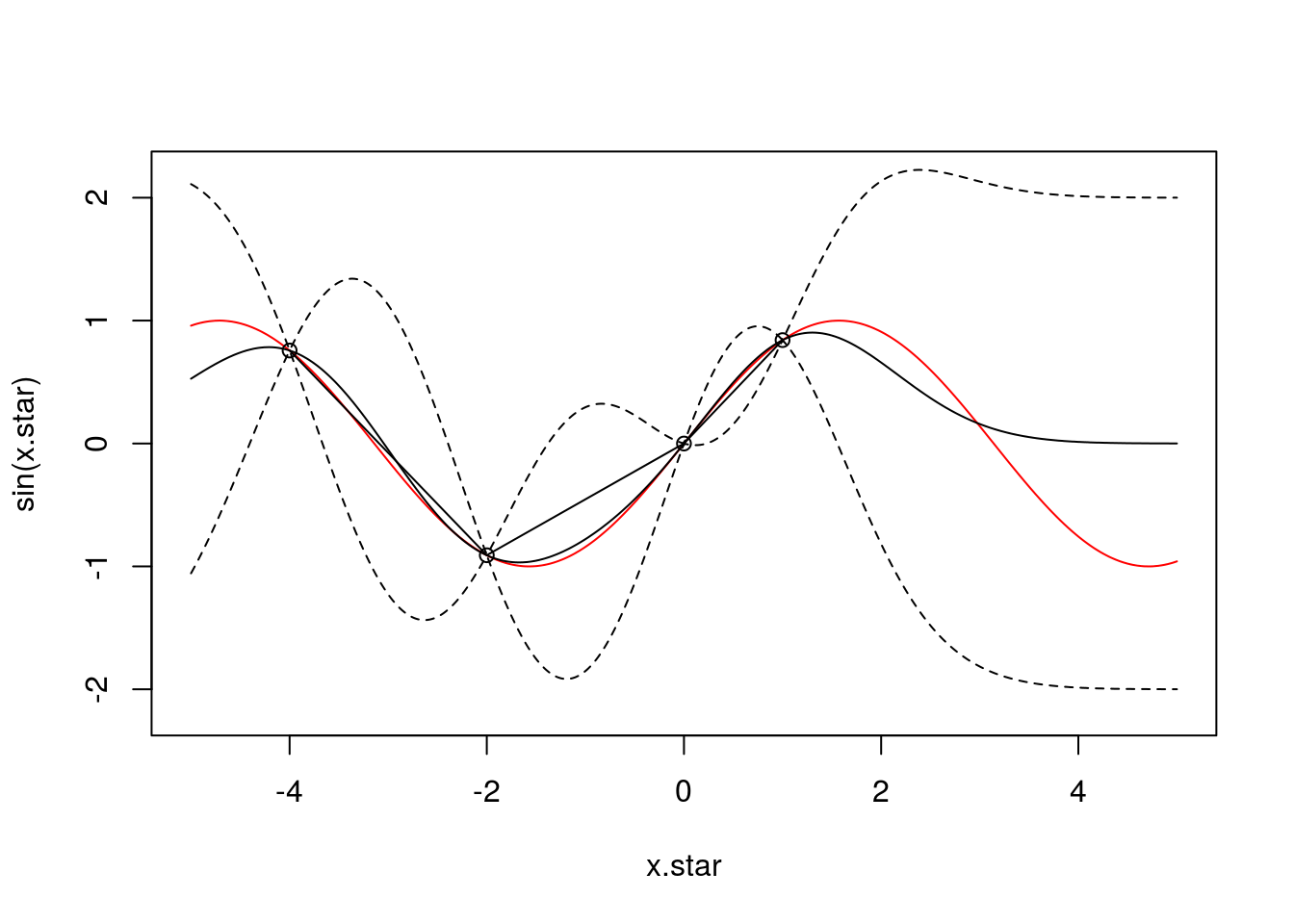
And with \(7\) observations:
f <- data.frame(x=c(-4,-3,-2,-1,0,1,2),
y=sin(c(-4,-3,-2,-1,0,1,2)))
x <- f$x
k.xx <- covSE(x,x)
k.xxs <- covSE(x,x.star)
k.xsx <- covSE(x.star,x)
k.xsxs <- covSE(x.star,x.star)
f.star.bar <- k.xsx%*%solve(k.xx)%*%f$y ###Mean
cov.f.star <- k.xsxs - k.xsx%*%solve(k.xx)%*%k.xxs ###Var
plot(x.star,sin(x.star),type = 'l',col="red",ylim=c(-2.2, 2.2))
points(f,type='o')
lines(x.star,f.star.bar,type = 'l')
lines(x.star,f.star.bar+2*sqrt(diag(cov.f.star)),type = 'l',pch=22, lty=2, col="black")
lines(x.star,f.star.bar-2*sqrt(diag(cov.f.star)),type = 'l',pch=22, lty=2, col="black")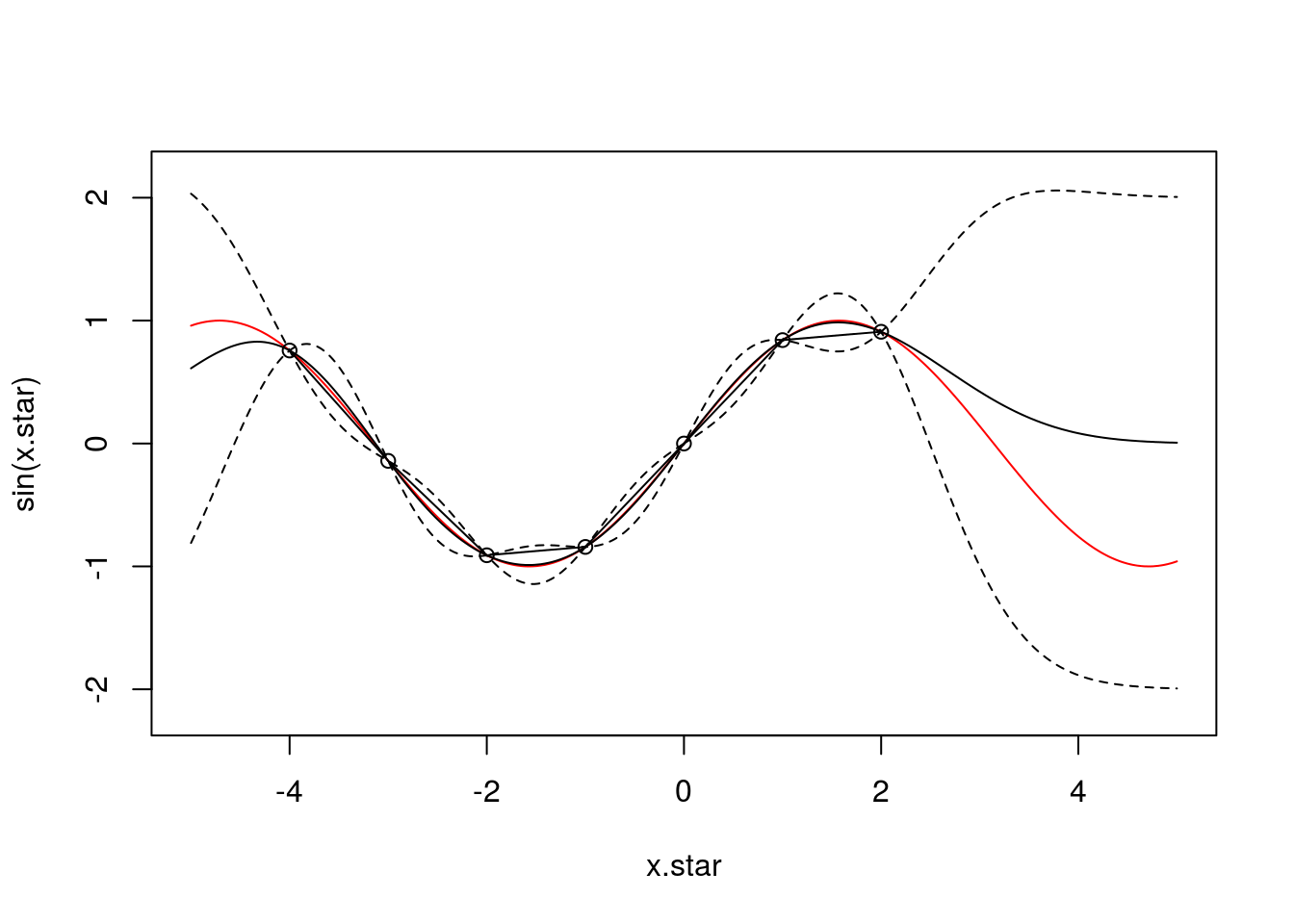
We can see that with \(7\) observations the posterior GP has begun to resemble the true (nonlinear) function very well: the mean of the GP lies very close to the true function and, perhaps more importantly, we continue to have an treatment for the uncertainty.
10.1.4.3 Marginal Likelihood and Optimisation of Hyperparameters
Another key aspect of GP regression is the ability to analytically evaluate the marginal likelihood, otherwise referred to as the “model evidence”. The marginal likelihood is the probability of generating the observed datasets under the specified prior. For a GP this would be the probability of seeing the observations \(\mathbf{X}\) under a Gaussian distribtion, \(\mathcal{N}(\mathbf{0},K(\mathbf{X},\mathbf{X}))\). The log marginal likelihood for a noise-free model is:
\(\ln p(\mathbf{y}|\mathbf{X}) = -\frac{1}{2}\mathbf{y}^\top [K(\mathbf{X},\mathbf{X})+\sigma_n^2\mathbb{I}]^{-1} \mathbf{y} -\frac{1}{2} \ln |K(\mathbf{X},\mathbf{X})+\sigma_n^2\mathbb{I}| - \frac{n}{2}\ln 2\pi\)
We calculate this in the snippet of code, below, hard-coding a small amount of Gaussian noise:
calcML <- function(f,l=1,sig=1) {
f2 <- t(f)
yt <- f2[2,]
y <- f[,2]
K <- covSE(f[,1],f[,1],l,sig)
ML <- -0.5*yt%*%ginv(K+0.1^2*diag(length(y)))%*%y -0.5*log(det(K)) -(length(f[,1])/2)*log(2*pi);
return(ML)
}The ability to calculate the marginal likelihood gives us a way to automatically select the hyperparameters. We can increment hyperparameters over a range of values, and choose the values that yield the greatest marginal likelihood. In the example, below, we increment both the length-scale and process variance hyperparameter:
library(plot3D)
par <- seq(.1,10,by=0.1)
ML <- matrix(rep(0, length(par)^2), nrow=length(par), ncol=length(par))
for(i in 1:length(par)) {
for(j in 1:length(par)) {
ML[i,j] <- calcML(f,par[i],par[j])
}
}
persp3D(z = ML,theta = 120)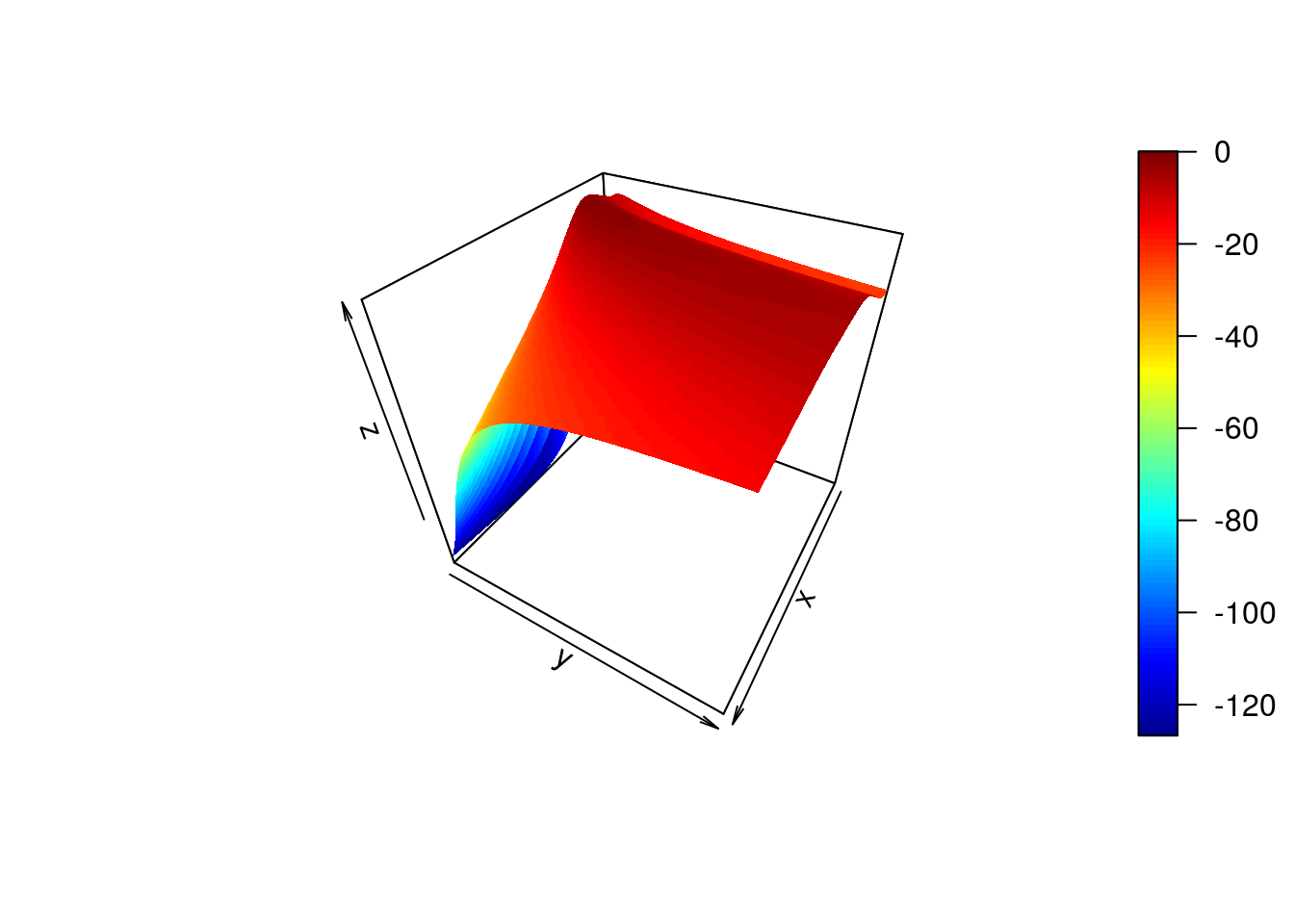
ind<-which(ML==max(ML), arr.ind=TRUE)
print(c("length-scale", par[ind[1]]))## [1] "length-scale" "2.4"print(c("process variance", par[ind[2]]))## [1] "process variance" "1.3"Here we have performed a grid search to identify the optimal hyperparameters. In practice, the derivative of the marginal likelihood with respect to the hyperparameters is analytically tractable, allowing us to optimise using gradient search algorithms.
Exercise 9.6: Try plotting the GP using the optimised hyperparameter values.
Exercise 9.7: Now try fitting a Gaussian process to one of the gene expression profiles in the Botrytis dataset. Hint: You may need to normalise the time axis. Since this data also contains a high level of noise you will also need to use a covariance function/ML calculation that incorporates noise. The snippet of code, below, does this, with the noise now representing a \(3\)rd hyperparameter.
covSEn <- function(X1,X2,l=1,sig=1,sigman=0.1) {
K <- matrix(rep(0, length(X1)*length(X2)), nrow=length(X1))
for (i in 1:nrow(K)) {
for (j in 1:ncol(K)) {
K[i,j] <- sig^2*exp(-0.5*(abs(X1[i]-X2[j]))^2 /l^2)
if (i==j){
K[i,j] <- K[i,j] + sigman^2
}
}
}
return(K)
}calcMLn <- function(f,l=1,sig=1,sigman=0.1) {
f2 <- t(f)
yt <- f2[2,]
y <- f[,2]
K <- covSE(f[,1],f[,1],l,sig)
ML <- -0.5*yt%*%ginv(K+diag(length(y))*sigman^2)%*%y -0.5*log(det(K+diag(length(y))*sigman^2)) -(length(f[,1])/2)*log(2*pi);
return(ML)
}10.1.4.4 Model Selection
As well as being a useful criterion for selecting hyperparameters, the marginal likelihood can be used as a basis for selecting models. For example, we might be interested in comparing how well we fit the data using two different covariance functions: a squared exponential covariance function (model 1, \(M_1\)) versus a periodic covariance function (model 2, \(M_2\)). By taking the ratio of the marginal likelihoods we can calculate the Bayes’ Factor (BF) which allows us to determine which model is the best:
\(\mbox{BF} = \frac{ML(M_1)}{ML(M_2)}\).
High values for the BF indicate strong evidence for \(M_1\) over \(M_2\), whilst low values would indicate the contrary.
Excercise: Using our previous example, \(y = sin(x)\) try fitting a periodic covariance function. How well does it generalise e.g., how well does it fit \(f(\cdot)\) far from the observation data? How does this compare to a squared-exponential?
10.1.4.5 Advanced application 1: differential expression of time series
Differential expression analysis is concerned with identifying if two sets of data are significantly different from one another. For example, if we measured the expression level of a gene in two different conditions (control versus treatment), you could use an appropriate statistical test to determine whether the expression of that gene had been affected by the treatment. Most statistical tests used for this are not appropriate when dealing with time series data (illustrated in Figure 10.1).
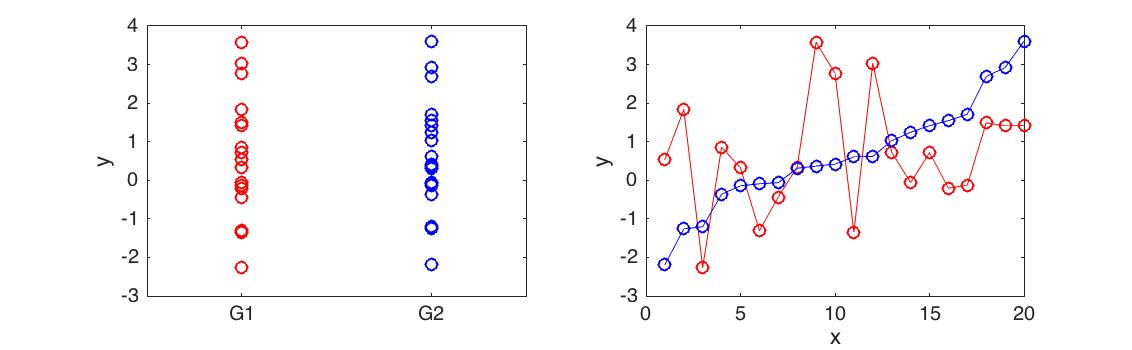
Figure 10.1: Differential expression analysis for time series. Here we have two time series with very different behaviour (right). However, as a whole the mean and variance of the time series is identical (left) and the datasets are not differentially expressed using a t-test (p<0.9901)
Gaussian processes regression represents a useful way of modelling time series, and can therefore be used as a basis for detecting differential expression in time series. To do so we write down two competing modes: (i) the two time series are differentially expressed, and are therefore best described by two independent GPs; (ii) the two time series are noisy observations from an identical underlying process, and are therefore best described by a single joint GP applied to the union of the data.
Exercise 9.8 (optional): Write a function for determining differential expression for two genes. Hint: you will need to fit \(3\) GPs: one to the mock/control, one to the infected dataset, and one to the union of mock/control and infected. You can use the Bayes’ Factor to determine if the gene is differentially expressed.
10.1.4.6 Scalability
Whilst GPs represent a powerful approach to nonlinear regression, they do have some limitations. GPs do not scale well with the number of observations, and standard GP approaches are not suitable when we have a very large datasets (thousands of observations). To overcome these limitations, approximate approaches to inference with GPs have been developed.
10.2 Classification
Classification algorithms are a supervised learning techniques that assign data to categorical outputs. For example we may have a continuous input variable, \(X\), and want to learn how that variable maps to a discrete valued output, \(y\in [0,1]\), which might represent two distinct phenotypes “infected” versus “uninfected”.
This section is split as follows: in section 10 we introduce logistic regression, a simple classification algorithm based on linear models; and in section @ref(#gp-classification) we demonstrate the use of nonlinear classifiers based on Gaussian process, highlighting when GP classifiers are more appropriate.
10.2.1 Logistic regression
The type of linear regression models we’ve been using up to this point deal with real-valued observation data, \(\mathbf{y}\), and are therefore not appropriate for classification. To deal with cases where \(\mathbf{y}\) is a binary outcome, we instead fit a linear model to the logit (natural log) of the log-odds ratio:
\(\ln \biggl{(}\frac{p(x)}{1-p(x)}\biggr{)} = c + m_1 x_1.\)
Although this model is not immediately intuitive, if we solve for \(p(x)\) we get:
\(p(x) = \frac{1}{1+\exp(-c - m_1 x_1)}\).
We have thus specified a function that indicates the probability of success for a given value of \(x\) e.g., \(P(y=1|x)\). Note that in our observation data \(\mathbf{y}\) itself can only take on one of two values. We can think of our data as a being a sample from a Bernoulli trial, and we can therefore write down the likelihood for a set of observations \({\mathbf{X},\mathbf{y}}\):
\(\mathcal{L}(c,m_1) = \prod_{i=1}^n p(x_i)^{y_i} (1-p(x_i)^{1-y_i})\).
In general, these models do not admit a closed form solution, but can be solved iteratively via maximum likelihood, that is by finding the values \((c,m_1)\) that return the greatest value of \(\mathcal{L}(c,m_1)\). Within {caret}, logistic regression can applied using the {glm} function.
To illustate this we will again make use of our plant dataset. Recall that the second column represents a binary variable indicative of infection status e.g., population growth of the Botrytis cinerea pathogen indicated by statistical enrichment of the Botrytis Tubulin versus the earliest time point.
In the excercises, below, we will aim to learn a set of markers capable of predicting infection status using logistic regression. To begin with, let’s see if time is informative of infection status:
library(pROC)## Type 'citation("pROC")' for a citation.##
## Attaching package: 'pROC'## The following objects are masked from 'package:stats':
##
## cov, smooth, varlibrary(ROCR)## Loading required package: gplots##
## Attaching package: 'gplots'## The following object is masked from 'package:stats':
##
## lowessoptions(warn=-1)
mod_fit <- train(y ~ ., data=data.frame(x = D$Time, y = as.factor(D$Class)), method="glm", family="binomial")To evaluate the model, we will load in a second (related) dataset, containnig a new set of observations not seen by the model, and predict infection status.
Dpred <- read.csv(file = "data/Arabidopsis/Arabidopsis_Botrytis_pred_transpose_3.csv", header = TRUE, sep = ",", row.names=1)
prob <- predict(mod_fit, newdata=data.frame(x = Dpred$Time, y = as.factor(Dpred$Class)), type="prob")
pred <- prediction(prob$`1`, as.factor(Dpred$Class))To evaluate how well the algorithm has done, we can calculate a variety of summary statistics. For example the number of true positives, true negatives, false positive and false negatives. A useful summary is to plot the ROC curve (false positive rate versus true positive rate) and calculate the area under the curve. For a perfect algorithm, the area under this curve (AUC) will be equal to \(1\), whereas random assignment would give an area of \(0.5\). In the example below, we will calculate the AUC for a logistic regression model:
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
plot(perf)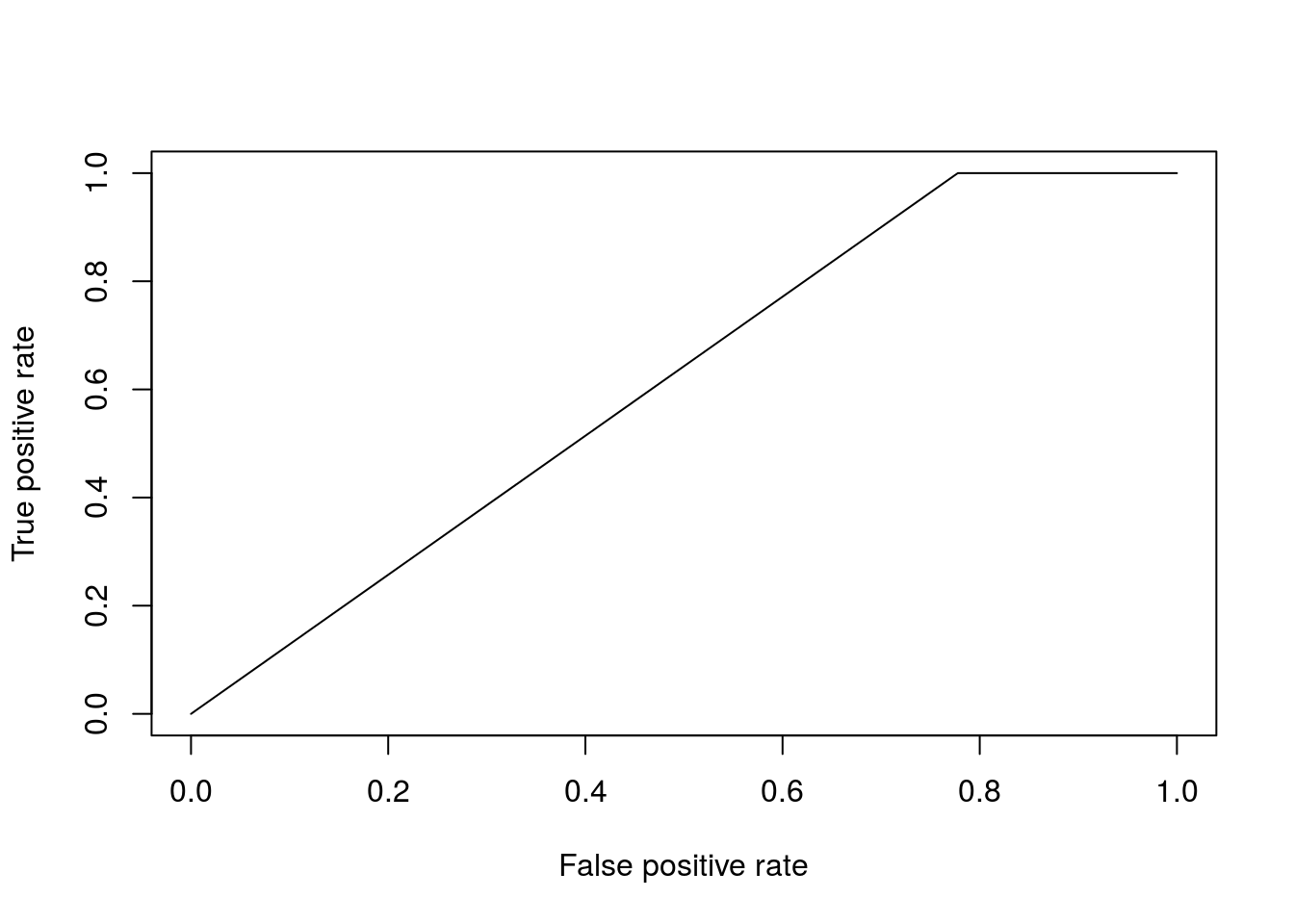
auc <- performance(pred, measure = "auc")
auc <- auc@y.values[[1]]
auc## [1] 0.6111111Okay, so a score of \(0.61\) is certainly better than random, but not particularly good. This is perhaps not surprising, as half the time series (the control) is uninfected over the entirety of the time series, whilst in the second times series Botrytis is able to infect from around time point 8 onwards. The slighty better than random performence therefore arises due the slight bias in the number of instances of each class.
In the example, below, we instead try to regress infection status against individual gene expression levels. The idea is to identify genes that have expression values indicative of Botrytis infection: marker genes.
aucscore <- matrix(rep(0, 164), 1, 164)
for (i in seq(3,164)){
mod_fit <- train(y ~ ., data=data.frame(x = D[,i], y = as.factor(D$Class)), method="glm", family="binomial")
prob <- predict(mod_fit, newdata=data.frame(x = Dpred[,i], y = as.factor(Dpred$Class)), type="prob")
pred <- prediction(prob$`1`, as.factor(Dpred$Class))
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
auc <- performance(pred, measure = "auc")
aucscore[i] <- auc@y.values[[1]]
}
plot(aucscore[1,3:ncol(aucscore)],ylab="AUC",xlab="gene index")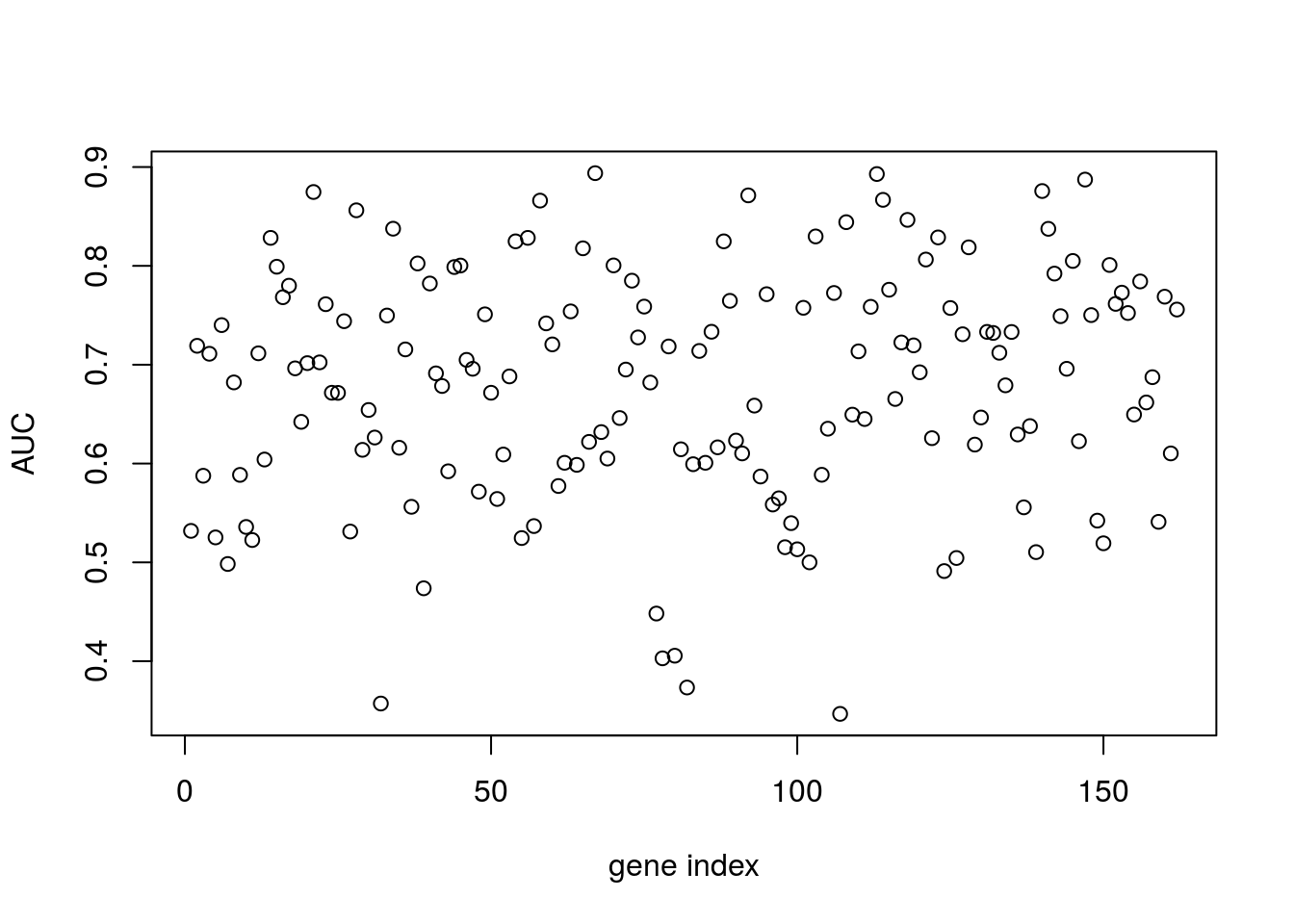
We note that, several genes in the list apear to have AUC scores much greater than \(0.6\). We can take a look at some of the genes with high predictive power:
genenames[which(aucscore>0.8)]## [1] "AT1G29990" "AT1G67170" "AT2G21380" "AT2G28890" "AT2G35500"
## [6] "AT2G45660" "AT3G09980" "AT3G11590" "AT3G13720" "AT3G25710"
## [11] "AT3G44720" "AT3G48150" "AT4G00710" "AT4G02150" "AT4G16380"
## [16] "AT4G19700" "AT4G26450" "AT4G28640" "AT4G34710" "AT4G36970"
## [21] "AT4G39050" "AT5G11980" "AT5G22630" "AT5G24660" "AT5G43700"
## [26] "AT5G50010" "AT5G56250"Unsurprisingly, amongst these genes we see a variety of genes whose proteins are known to be targeted by various pathogen effectors, and are therefore directly implicated in the immune response (Table 3.1).
| Gene | Effector |
|---|---|
| AT3G25710 | ATR1_ASWA1 |
| AT4G19700 | ATR13_NOKS1 |
| AT4G34710 | ATR13_NOKS1 |
| AT4G39050 | ATR13_NOKS1 |
| AT5G24660 | ATR13_NOKS1 |
| AT4G00710 | AvrRpt2_Pto JL1065_CatalyticDead |
| AT4G16380 | HARXL44 |
| AT2G45660 | HARXL45 |
| AT5G11980 | HARXL73 |
| AT2G35500 | HARXLL445 |
| AT1G67170 | HARXLL470_WACO9 |
| AT4G36970 | HARXLL470_WACO9 |
| AT5G56250 | HARXLL470_WACO9 |
| AT3G09980 | HARXLL516_WACO9 |
| AT5G50010 | HARXLL60 |
| AT3G44720 | HARXLL73_2_WACO9 |
| AT5G22630 | HARXLL73_2_WACO9 |
| AT5G43700 | HopH1_Psy B728A |
Table 3.1: Genes predictive of infection status of Botrytis cinerea whose proteins are targeted by effectors of a variety of pathogens
Let’s take a look at what the data looks like. In this case we plot the training data labels and the fit from the logistic regression i.e., \(p(\mathbf{y}=1|\mathbf{x})\):
bestpredictor <- which(aucscore==max(aucscore))
best_mod_fit <- train(y ~., data=data.frame(x = D[,bestpredictor], y = as.factor(D$Class)), family="binomial", method="glm")
plot(D[,bestpredictor],D$Class,xlab=genenames[bestpredictor],ylab="Class")
lines(seq(min(D[,bestpredictor]),max(D[,bestpredictor]),length=200),predict(best_mod_fit,newdata=data.frame(x = seq(min(D[,bestpredictor]),max(D[,bestpredictor]),length=200)),type="prob")[,2])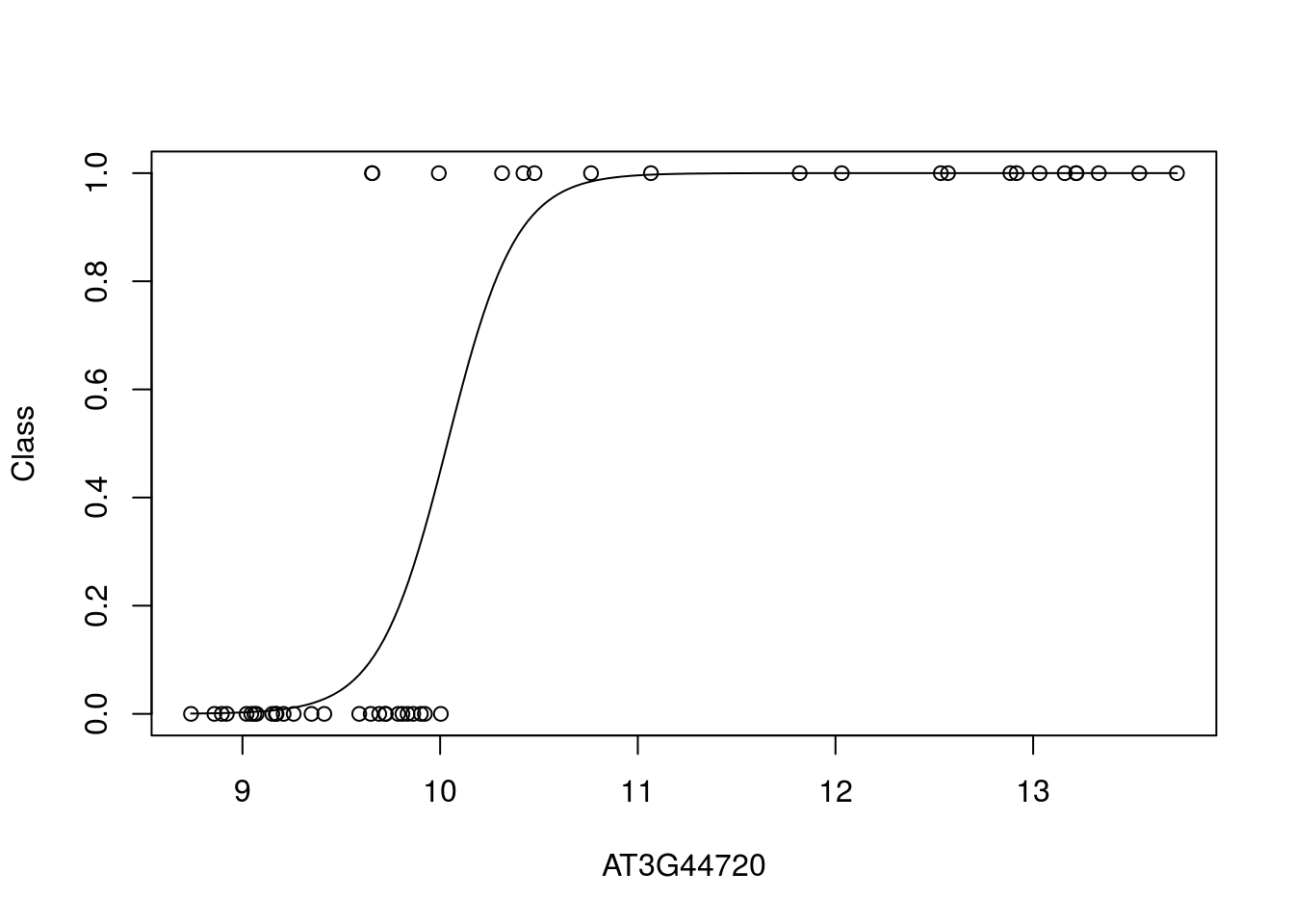
10.2.2 GP classification
Classification approaches using Gaussian processes are also possible. Unlike Gaussian process regression, Gaussian process classification is not analytically tractable, and we must instead use approximations. A GP classifier has been implemented in {caret} using a polynomial kernel, and can be called using the following code:
mod_fit2 <- train(y~., data=data.frame(x = D$Time, y = as.factor(D$Class)), method="gaussprPoly")Again, we can systematically evaluate how well different genes predict the observed phenotype.
library(kernlab)##
## Attaching package: 'kernlab'## The following object is masked from 'package:ggplot2':
##
## alphaaucscore2 <- matrix(rep(0, 164), 1, 164)
for (i in seq(3,164)){
mod_fit2 <- gausspr(D[,i], as.factor(D$Class), scaled = TRUE, type= NULL, kernel="rbfdot", kpar="automatic", variance.model = FALSE, tol=0.0005, cross=0, fit=TRUE)
prob<-predict(mod_fit2, Dpred[,i], type="probabilities")
pred <- prediction(prob[,2], as.factor(Dpred$Class))
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
auc <- performance(pred, measure = "auc")
aucscore2[i] <- auc@y.values[[1]]
}## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernel
## Using automatic sigma estimation (sigest) for RBF or laplace kernelWe can compare the performence against the logistic regression:
plot(t(aucscore),t(aucscore2),xlab="Logistic",ylab="GP")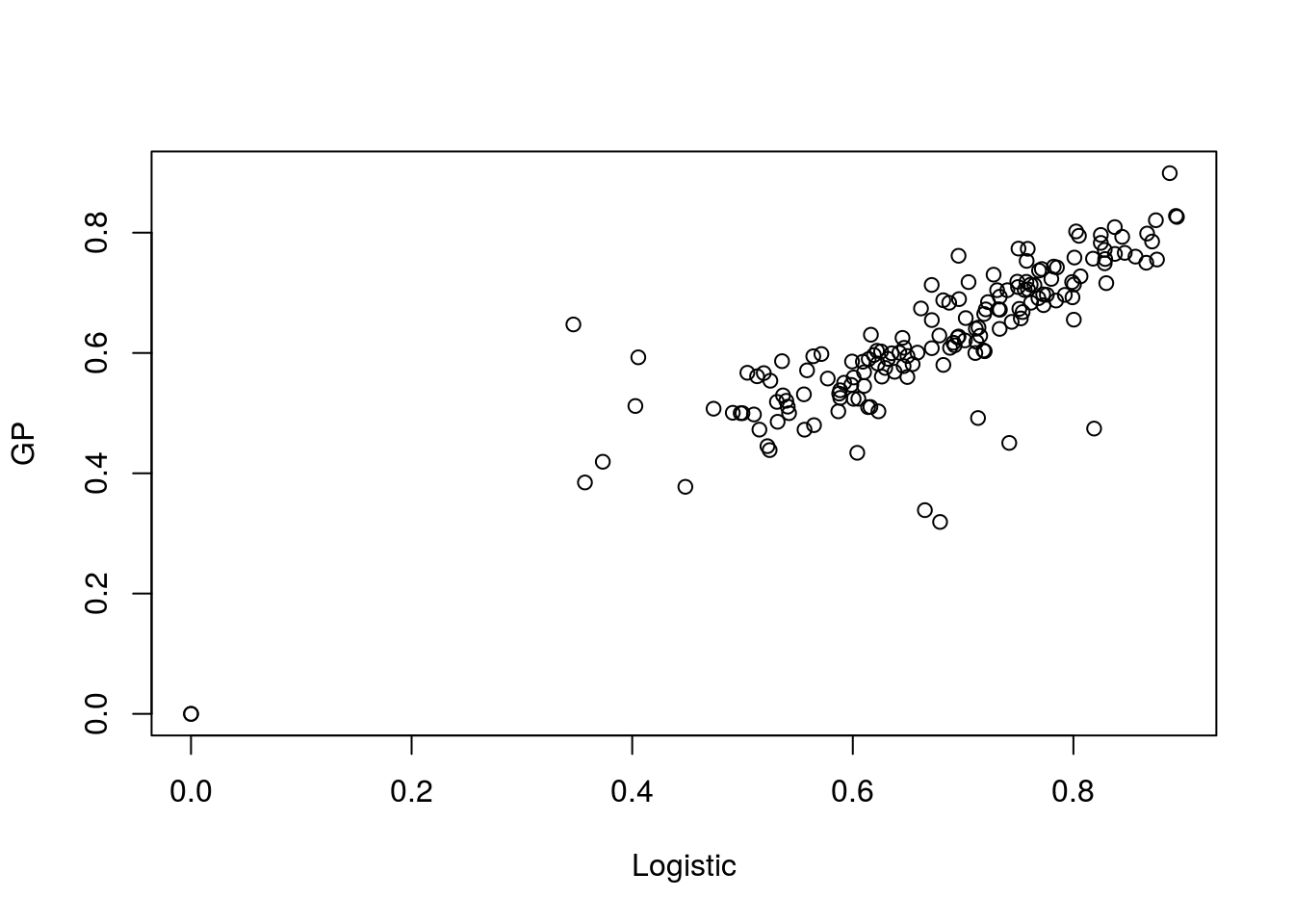
Note that the results are similar. Dissapointingly similar. We have gone to the effort to utilise a far more powerful method yet the empircal results are no better.
The power of GPs and other nonlinear approaches will not be clear unless the data is nonlinear. To illustrate this we will construct an artifical dataset in which low expression levels of a gene indicates no infection, with moderate levels indicating infection; very high levels of the gene, however, do not indicate infected status, but only arise artifically, due to e.g., inducible overexpression. For this dataset very high levels are thus labelled as uninfected. Below we construct this in silico dataset based loosley on the expression levels of AT3G44720.
xtrain = D[,bestpredictor]
ytrain = as.numeric(D$Class)
ytrain[which(xtrain>12.5)]=0
ytrain[which(xtrain<10)]=0
ytrain = as.factor(ytrain)
xpred = Dpred[,bestpredictor]
ypred = as.numeric(Dpred$Class)
ypred[which(xpred>12.5)]=0
ypred[which(xpred<10)]=0
ypred = as.factor(ypred)Let’s first fit a logistic model and visualise the result:
mod_fit3 <- train(y ~., data=data.frame(x = xtrain, y= as.factor(ytrain)), family="binomial", method = "glm")
plot(xtrain,as.numeric(ytrain)-1,xlab="Marker gene",ylab="Class")
lines(seq(min(xtrain),max(xtrain),length=200),predict(mod_fit3,newdata=data.frame(x = seq(min(xtrain),max(xtrain),length=200),y= matrix(200,1,1)),type="prob")[,2])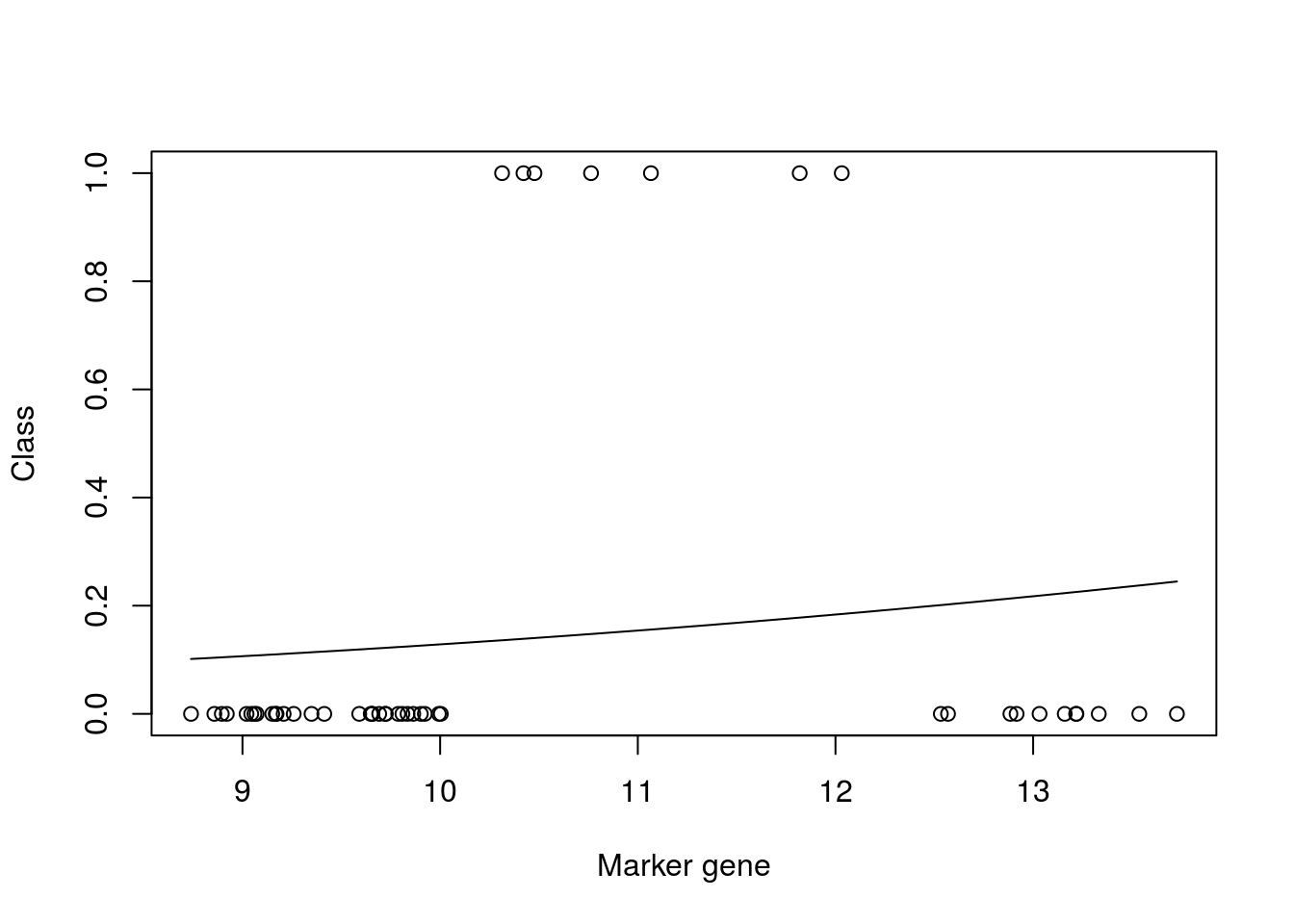
mod_fit3$results$Accuracy## [1] 0.8660466We can see from the plot that the model fit is very poor. However, if we look at the accuracy (printed at the bottom) the result appears to be good. This is due to the skewed number of samples from each class: there are far more non infected samples than there are infected, which means that if the model predicts uninfected for every instance, it will be correct more than it’s incorrect. We can similary check the result on our test dataset:
prob<-predict(mod_fit3, newdata=data.frame(x =xpred, y = as.factor(ypred)), type="prob")
pred <- prediction(prob[,2], ypred)
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
auc <- performance(pred, measure = "auc")
auc <- auc@y.values[[1]]
auc## [1] 0.7104377We can now instead attempt to take advantage the extra flexibility of GPs.
mod_fit2 <- gausspr(y~x,x=xtrain, y=ytrain, scaled = TRUE, type= NULL, kernel="rbfdot", kpar="automatic", variance.model = FALSE, tol=0.0005, cross=0, fit=TRUE)## Using automatic sigma estimation (sigest) for RBF or laplace kernelplot(xtrain,as.numeric(ytrain)-1,xlab="Marker gene",ylab="Class")
lines(seq(min(xtrain),max(xtrain),length=200),predict(mod_fit3,newdata=data.frame(x = seq(min(xtrain),max(xtrain),length=200),y= matrix(200,1,1)),type="prob")[,2])
lines(seq(min(xtrain),max(xtrain),length=200),predict(mod_fit2,seq(min(xtrain),max(xtrain),length=200), type="prob")[,2],col="red")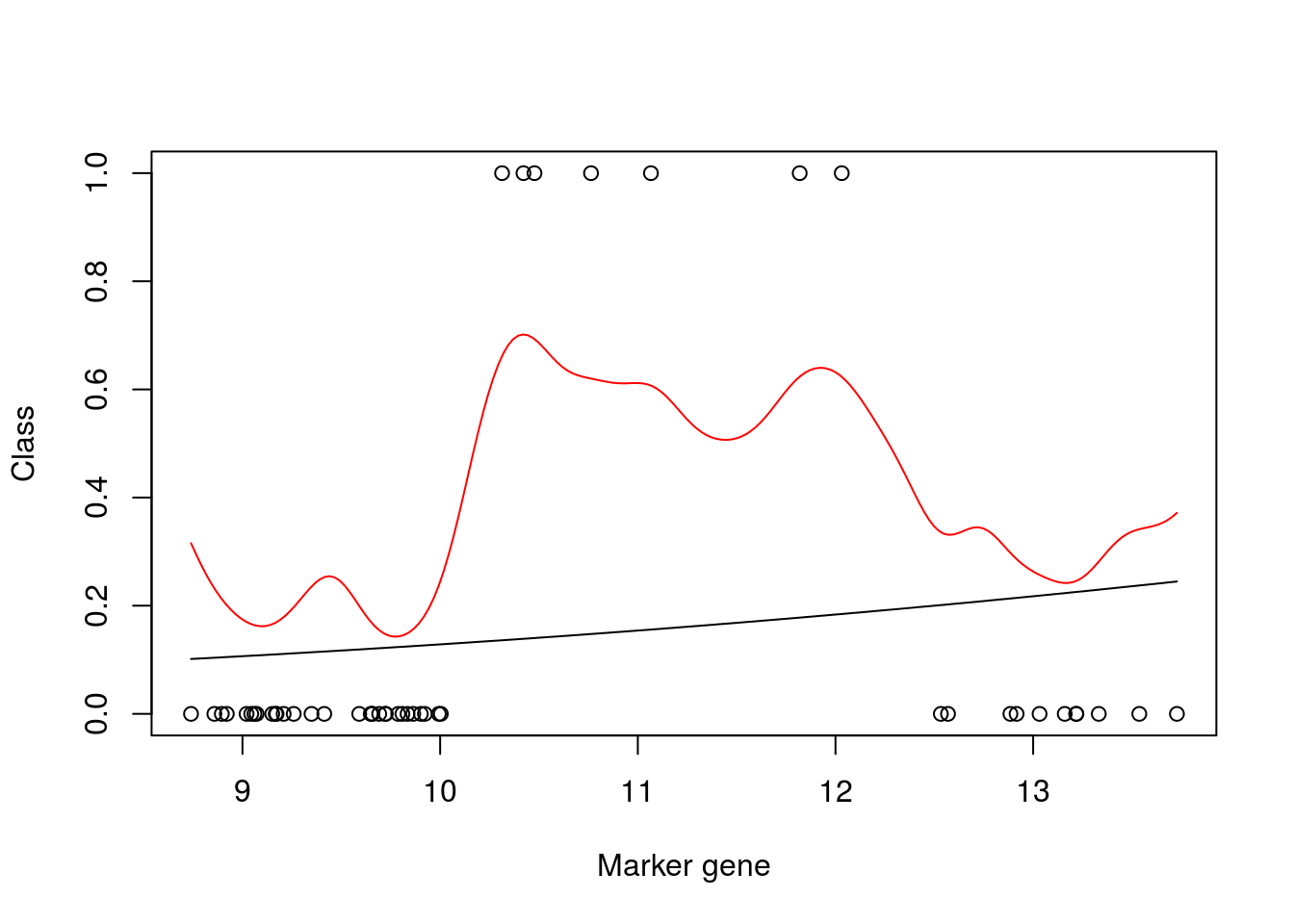
prob2<-kernlab::predict(mod_fit2, newdata=data.frame(x =xpred), type="probabilities")
prob<-predict(mod_fit2, xpred, type="probabilities")
pred <- prediction(prob2[,2], ypred)
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
auc <- performance(pred, measure = "auc")
auc <- auc@y.values[[1]]
auc## [1] 0.8193042Boom! We can see that this is a much better model, both in terms of the model fit, which has found a nonlinear classifier, and in terms of the AUC score.
10.2.3 Other classification approaches.
Quite often in ML we are interested in predicting class labels with maximum accuracy. That is, we are less concerned about intepreting what our function says about the system, and are only interested in our ability to predict \(\mathbf{y}*\) at the new locations \(\mathbf{X}*\).
A variety of classifiers are availble in {caret}, including those based on random forests and support vector machines, as well as those based on neural networks. In the examples, below, we use some of these approaches to predict infection status from expression data.
library("stepPlr")
library("party")## Loading required package: grid## Loading required package: mvtnorm## Loading required package: modeltools## Loading required package: stats4##
## Attaching package: 'modeltools'## The following object is masked from 'package:kernlab':
##
## prior## The following object is masked from 'package:plyr':
##
## empty## The following object is masked from 'package:lme4':
##
## refit## Loading required package: strucchange## Loading required package: zoo##
## Attaching package: 'zoo'## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric## Loading required package: sandwichlibrary("kernlab")
mod_fit1 <- train(y ~ x, data=data.frame(x = D$AT3G44720, y = as.factor(D$Class)), method="plr")##
## Convergence warning in plr: 6#mod_fit2 <- train(y ~ x, data=data.frame(x = D$AT3G44720, y = as.factor(D$Class)), method="cforest")
mod_fit3 <- train(y ~ x, data=data.frame(x = D$AT3G44720, y = as.factor(D$Class)), method="svmRadialWeights")Although we can run a variety of algorithms and check the accuracy of their predictions seperately, another approach would be to combine predicitons to achieve increased accuracy. More information on ensemble learning is available from CRAN.
10.3 Resources
A variety of examples using {caret} to perform regression and classification have been implemented here.
More comprehensive Gaussian process packages are available including the Matlab package GPML, and Python package GPy. GP code based on Tensorflow is also available in the form of GPflow and GPflowopt.
Coming soon GPflow for R
======= ## Exercises
Solutions to exercises can be found in appendix I.
K Solutions for use case 2
Windram, Oliver, Priyadharshini Madhou, Stuart McHattie, Claire Hill, Richard Hickman, Emma Cooke, Dafyd J Jenkins, et al. 2012. “Arabidopsis Defense Against Botrytis Cinerea: Chronology and Regulation Deciphered by High-Resolution Temporal Transcriptomic Analysis.” The Plant Cell 24 (9). Am Soc Plant Biol: 3530–57.
Williams, Christopher KI, and Carl Edward Rasmussen. 2006. Gaussian Processes for Machine Learning. Vol. 2. the MIT Press.